Advertisements
Advertisements
Question
Answer the following question.
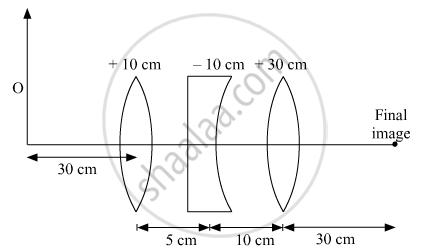
Three lenses of focal length +10 cm, —10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination.

Solution
`1/v - 1/u = 1/f`
`u = -30 cm`
`f = +10 cm`
`1/nu = 1/f + 1/u`
`1/nu_1 = 1/10 - 1/30`
⇒ `1/nu_1 = (3 - 1)/30 = 2/30`
`nu_1 = 15` cm
`u = +10 cm`
`f = -10 cm`
`1/nu_2 = 1/f + 1/u = 1/10 - 1/10`
`nu_2 = ∞`
For third lens object is at infinity hence image is formed at focus final image at a distance of 30 cm.
RELATED QUESTIONS
Can mirrors give rise to chromatic aberration?
A man uses a concave mirror for shaving. He keeps his face at a distance of 25 cm from the mirror and gets an image which is 1.4 times enlarged. Find the focal length of the mirror.
Light is incident from glass (μ = 1.5) to air. Sketch the variation of the angle of deviation δ with the angle of incident i for 0 < i < 90°.
The focal length of a convex lens made of glass of refractive index (1.5) is 20 cm.
What will be its new focal length when placed in a medium of refractive index 1.25?
Is focal length positive or negative? What does it signify?
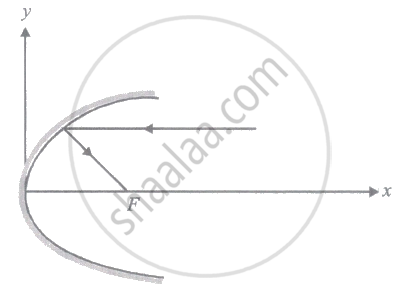
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
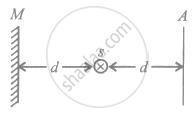
The intensity of a point source of light, S, placed at a distance d in front of a screen A, is I0 at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror M is placed at a distance d behind the source, as shown in the figure.
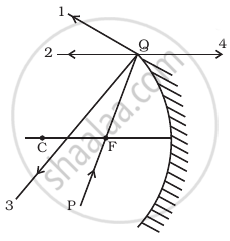
The direction of ray of light incident on a concave mirror is shown by PQ while directions in which the ray would travel after reflection is shown by four rays marked 1, 2, 3 and 4 (figure). Which of the four rays correctly shows the direction of reflected ray?
A concave mirror of focal length 12 cm forms three times the magnified virtual image of an object. Find the distance of the object from the mirror.
Why does a car driver use a convex mirror as a rear-view mirror?
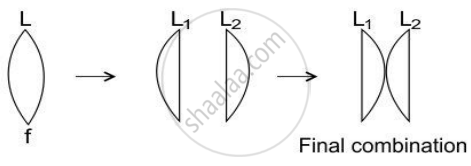
A lens of focal length f is divided into two equal parts and then these parts are put in a combination as shown in the figure below.
- What is the focal length of L1?
- What is the focal length of the final combination?