Advertisements
Advertisements
Question
तीन शीर्षों A(–2, 3), B(6, 7) और C(8, 3) वाले समांतर चतुर्भुज ABCD का चौथा शीर्ष D ______ हैं।
Options
(0, 1)
(0, –1)
(–1, 0)
(1, 0)
Solution
तीन शीर्षों A (– 2, 3), B(6, 7) और C(8, 3) वाले समांतर चतुर्भुज ABCD का चौथा शीर्ष D (0, –1) हैं।
स्पष्टीकरण:
माना समांतर चतुर्भुज का चौथा शीर्ष, D ≡ (x4 ,y4) और L, M क्रमशः AC और BD के मध्य बिंदु हैं,
फिर, `L ≡ ((-2 + 8)/2, (3 + 3)/2) ≡ (3, 3)` और `M ≡ ((6 + x_4)/2, (7 + "y"_4)/2)` ...`["चूंकि बिंदु" (x_1, y_1) "और" (x_2, y_2) "वाले रेखा खंड के मध्य बिंदु" = ((x_1 + x_2)/2, (y_1 + y_2)/2)]`
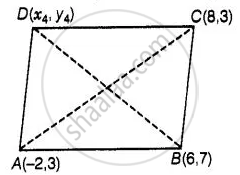
चूँकि, ABCD एक समांतर चतुर्भुज है, इसलिए विकर्ण AC और BD एक दूसरे को समद्विभाजित करेंगे।
इसलिए, L और M समान बिंदु हैं।
∴ 3 = `(6 + x_4)/2` and 3 = `(7 + y_4)/2`
⇒ 6 = 6 + x4 and 6 = 7 + y4
⇒ x4 = 0 and y4 = 6 – 7
∴ x4 = 0 and y4 = –1
अतः, समांतर चतुर्भुज का चौथा शीर्ष D = (x4, y4) = (0, –1) है।
APPEARS IN
RELATED QUESTIONS
यदि बिंदु L(x, 7) और M(1, 15) के बीच की दूरी 10 हो, तो x का मान ज्ञात कीजिए।
सिद्ध कीजिए कि, A(-4, -7), B(-1, 2), C(8, 5) और D(5, -4) समचतुर्भुज ABCD के शीर्ष बिंदु हैं।
किसी त्रिभुज के शीर्षबिंदु A(-3,1), B(0,-2) और C(1,3) हों तो इस त्रिभुज के परिकेंद्र के निर्देशांक ज्ञात कीजिए।
निम्नलिखित बिंदुओं को जोड़नेवाले रेखाखंड त्रिभुज बना सकते हैं क्या? यदि त्रिभुज बनता हो तो भुजाओं के आधार पर त्रिभुज का प्रकार लिखिए।
L(6, 4), M(-5, -3), N(-6, 8)
यदि Q(0, 1) बिंदुओं P(5, –3) और R(x, 6) से समदूरस्थ है, तो x के मान ज्ञात कीजिए। दूरियाँ QR और PR भी ज्ञात कीजिए।
बिंदु P(–6, 8) की मूलबिंदु से दूरी ______ है।
बिंदुओं A(1, 5) और B(4, 6) को मिलाने वाले रेखाखंड का लंब समद्वि भाजक y-अक्ष को निम्नलिखित बिंदु पर काटता ______ हैं।
शीर्षों A(– 2, 0), B(2, 0) और C(0, 2) वाला त्रिभुज ABC शीर्षों D(–4, 0), E(4, 0) और F(0, 4) वाले त्रिभुज DEF के समरूप है।
x-अक्ष पर स्थित ऐसे बिंदु ज्ञात कीजिए, जो बिंदु (7, – 4) से `2sqrt(5)` की दूरी पर हैं। ऐसे कितने बिंदु हैं?
a का मान ज्ञात कीजिए, यदि बिंदुओं A(–3, –14) और B(a, –5) के बीच की दूरी 9 इकाई है।
