Advertisements
Advertisements
Question
शीर्षों A(– 2, 0), B(2, 0) और C(0, 2) वाला त्रिभुज ABC शीर्षों D(–4, 0), E(4, 0) और F(0, 4) वाले त्रिभुज DEF के समरूप है।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण:
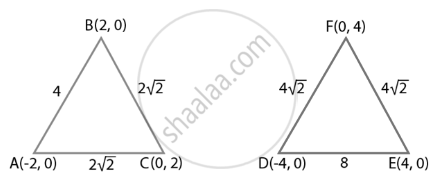
दूरी के सूत्र का प्रयोग करके,
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
हम ढूंढ सकते हैं,
AB = `sqrt((2 + 2)^2 + 0) = sqrt(16)` = 4
BC = `sqrt((0 - 2)^2 + (2 - 0)^2) = sqrt(8) = 2sqrt(2)`
CA = `sqrt((-2 - 0)^2 + (0 - 2)^2) = sqrt(8) = 2sqrt(2)`
DE = `sqrt((4 + 4)^2 + 0) = sqrt(64)` = 8
EF = `sqrt((0 - 4)^2 + (4 - 0)^2) = sqrt(32) = 4sqrt(2)`
FD = `sqrt((-4 - 0)^2 + (0 - 4)^2) = sqrt(32) = 4sqrt(2)`
∴ `("AB")/("DE") = ("BC")/("EF") = ("CA")/("FD") = 1/2`
⇒ ΔABC ∼ ΔDEF
अतः, त्रिभुज ABC और DEF समरूप हैं।
APPEARS IN
RELATED QUESTIONS
सिद्ध कीजिए कि, A(1, 2), B(1, 6), C(1 + `2sqrt3`, 4) समबाहु त्रिभुज के शीर्ष बिंदु हैं।
नीचे दिए गए बिंदु एकरेखीय हैं या नहीं? इसकी जाँच कीजिए।
L(-2, 3), M(1, -3), N(5, 4)
सिद्ध कीजिए कि, P(2, -2), Q(7, 3), R(11, -1) और S(6, -6) समांतर चर्तुभुज के शीर्षबिंदु है।
किसी कक्षा में, चार मित्र बिंदुओं A, B, C और D पर बैठे हुए हैं, जैसाकि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, 'क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?' चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें कौन सही है?
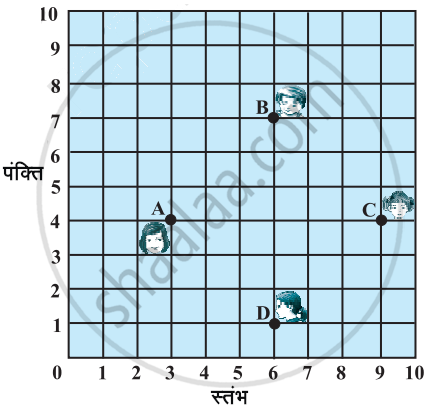
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(-3, 5), (3, 1), (0, 3), (-1, -4)
किसी वर्ग के दो सम्मुख शीर्ष (-1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।
शीर्षों (0, 4), (0, 0) और (3, 0) वाले त्रिभुज का परिमाप ______ है।
मूलबिंदु को केंद्र मान कर खींचा गया एक वृत्त बिंदु `(13/2, 0)` से होकर जाता है। तब, वृत्त के अभ्यंतर में निम्नलिखित बिंदु स्थित नहीं ______ है।
बिंदु A(2, 7), बिंदुओं P(6, 5) और Q(0, – 4) को मिलाने वाले रेखाखंड के लंब समद्विभाजक पर स्थित है।
बिंदुओं A(2, –2), B(7, 3), C(11, –1) और D(6, –6) को इसी क्रम में लेने पर किस प्रकार का चतुर्भुज बनता है?
