Advertisements
Advertisements
Question
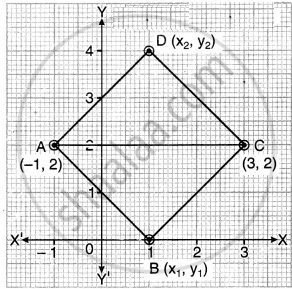
किसी वर्ग के दो सम्मुख शीर्ष (-1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।
Advertisements
Solution
वर्ग ABCD में दो सम्मुख शीर्ष A(-1, 2) एवं C(3, 2) दिए हैं। मान लीजिए B (x1, y1) एवं D (x2, y2) दो अन्य शीर्ष हैं।
AB = BC (वर्ग की भुजाएँ)
`sqrt((x_1 + 1)^2 + (y_1 - 2)^2) = sqrt((x_1 - 3)^2 + (y_1 - 2)^2)`
⇒ (x1 + 1)2 + (y1 - 2)2 = (x1 - 3)2 + (y1 - 2)2 (दोनों ओर वर्ग करने पर)
⇒ (x1 + 1)2 = (x1 - 3)2
⇒ x12 + 2x1 + 1 = x12 - 6x1 + 9
⇒ 2x1 + 6x1 = 9 - 1
⇒ 8x1 = 8
⇒ x1 = 88 = 1 ….(1)
∵ AB2 + BC2 = AC2 (समकोण ∆ABC में पाइथागोरस प्रमेय से)
⇒ (x1 + 1)2 + (y1 - 2)2 + (x1 - 3)2 + (y1 - 2)2 = (3 + 1)2 + (2 - 2)2
⇒ x12 + 2x1 + 1 + y12 – 4y1 + 4 + x12 - 6x1 + 9 + y12 - 4y1 + 4 = 16 - 0
⇒ 2x12 + 2y12 - 4x1 - 8y1 = 16 - 18 = -2
⇒ x12 + y12 - 2x1 - 4y1 + 1 = 0 …(2)
⇒ x1 = 1 का मान समीकरण (1) से समीकरण (2) में रखने पर,
⇒ (1)2 + (y1)2 - 2 (1) - 4y1 + 1 = 0
⇒ y12 - 4y1 = 0
⇒ y1 (y1 - 4) = 0
या तो y1 = 0 अथवा y1 - 4 = 0
⇒ y1 = 4
B के निर्देशांक (1, 0) अथवा (1, 4) हैं।
AD = DC (वर्ग की भुजाएँ हैं)
⇒ `sqrt((x_2 + 1)^2 + (y_2 - 2)^2) = sqrt((x_2 - 3)^2 + (y_2 - 2)^2)`
⇒ (x2 + 1)2 + (y2 - 2)2 = (x2 - 3)2 + (y2 - 2)2 (दोनों ओर वर्ग करने पर)
⇒ (x2 + 1)2 = (x2 - 3)2
⇒ x22 + 2x2 + 1 = x22 - 6x2 + 9
⇒ 8x2 = 8
⇒ x2 = `8/8` = 1 . …(3)
AD2 + CD2 = AC2 (समकोण ∆ADC में पाइथागोरस प्रमेय से)
⇒ (x2 + 1)2 + (y2 - 2)2 + (x2 - 3)2 + (y2 - 2)2 = (3 + 1)2 + (2 - 2)2
⇒ x22 + 2x2 + 1 + y22 - 4y2 + 4 + x22 - 6x2 + 9 + y22 - 4y2 + 4 = 16 + 0
⇒ 2x22 + 2y22 - 4x2 - 8y2 = 16 - 18 = -2
⇒ x22 + y22 – 2x2 - 4y2 + 1 = 0 ….(4)
x2 = 1 का मान समीकरण (3) से समीकरण (4) में रखने पर,
⇒ (1)² + y22 - 2 (1) - 4y2 + 1 = 0
⇒ 1 + y22 - 2 - 4y2 + 1 = 0
⇒ y22 - 4y2 = 0
⇒ y2 (y2 - 4) = 0
या तो y2 = 0 अथवा y2 - 4 = 0
⇒ y2 = 4
D के निर्देशांक (1, 0) अथवा (1, 4)
अतः अभीष्ट शीर्षों के निर्देशांक क्रमशः (1, 0) एवं (1, 4) हैं।
RELATED QUESTIONS
नीचे दिए गए बिंदु एकरेखीय हैं या नहीं? इसकी जाँच कीजिए।
A(1, −3), B(2, −5), C(−4, 7)
जाँच कीजिए कि बिंदु P(-2, 2), Q(2, 2) और R(2, 7) समकोण त्रिभुज के शीर्षबिंदु हैं।
निम्नलिखित बिंदुओं को जोड़नेवाले रेखाखंड त्रिभुज बना सकते हैं क्या? यदि त्रिभुज बनता हो तो भुजाओं के आधार पर त्रिभुज का प्रकार लिखिए।
P(-2, -6), Q(-4, -2), R(-5, 0)
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(-1, -2,), (1, 0), (-1, 2), (-3, 0)
x-अक्ष पर वह बिंदु ज्ञात कीजिए जो (2, -5) और (-2, 9) से समदूरस्थ हैं।
x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु (x, y) बिंदुओं (3, 6) और (–3, 4) से समदूरस्थ हो।
शीर्षों A(– 2, 0), B(2, 0) और C(0, 2) वाला त्रिभुज ABC शीर्षों D(–4, 0), E(4, 0) और F(0, 4) वाले त्रिभुज DEF के समरूप है।
बिंदु A(4, 3), B(6, 4), C(5, –6) और D(–3, 5) एक समांतर चतुर्भुज के शीर्ष हैं।
x-अक्ष पर स्थित ऐसे बिंदु ज्ञात कीजिए, जो बिंदु (7, – 4) से `2sqrt(5)` की दूरी पर हैं। ऐसे कितने बिंदु हैं?
किसी वृत्त का केन्द्र (2a, a – 7) है। यदि वृत्त, बिंदु (11, – 9) से होकर जाता है और उसका व्यास `10sqrt(2)` इकाई है, तो a के मान ज्ञात कीजिए।
