Advertisements
Advertisements
Question
बिंदु A(2, 7), बिंदुओं P(6, 5) और Q(0, – 4) को मिलाने वाले रेखाखंड के लंब समद्विभाजक पर स्थित है।
Options
सत्य
असत्य
Solution 1
यह कथन असत्य है।
स्पष्टीकरण:
यदि A(2, 7) P(6, 5) और Q(0, – 4) के लंबवत समद्विभाजक पर स्थित है,
तब AP = AQ
∴ AP = `sqrt((6 - 2)^2 + (5 - 7)^2`
= `sqrt((4)^2 + (-2)^2`
= `sqrt(16 + 4)`
= `sqrt(20)`
और A = `sqrt((0 - 2)^2 + (-4 - 7)^2`
= `sqrt((-2)^2 + (-11)^2`
= `sqrt(4 + 121)`
= `sqrt(125)`
अतः, A, PQ के लंब समद्विभाजक पर स्थित नहीं है।
Solution 2
यह कथन असत्य है।
स्पष्टीकरण:
यदि बिंदु A(2, 7) रेखा खंड के लंबवत समद्विभाजक पर स्थित है, तो बिंदु A लंबवत समद्विभाजक के समीकरण को संतुष्ट करता है।
अब, हम लंब समद्विभाजक का समीकरण ज्ञात करते हैं।
इसके लिए हम लंब समद्विभाजक का ढलान ज्ञात करते हैं।
∴ लम्ब समद्विभाजक का ढलान = `(-1)/("बिंदुओं को जोड़ने वाले रेखाखंड का ढलान" (5, -3) "और" (0, -4))`
= `(-1)/((-4 - (-3))/(0 - 5))` ...`[∵ "ढलान" = (y_2 - y_1)/(x_2 - x_1)]`
= 5
[चूंकि, लंब समद्विभाजक रेखा खंड पर लंबवत है, इसलिए इसकी ढलान की स्थिति है, m1 · m2 = – 1]
चूंकि, लंब समद्विभाजक बिंदुओं (5, – 3) और (0, – 4) को मिलाने वाले रेखाखंड के मध्य-बिंदु से होकर गुजरता है।
∴ PQ का मध्य-बिंदु = `((5 + 0)/2, (-3 - 4)/2) = (5/2, (-7)/2)`
तो, लम्ब समद्विभाजक का समीकरण जिसका ढलान `1/3` है और मध्य-बिंदु `(5/2, (-7)/2)` से होकर गुजरता है।
`(y + 7/2) = 5(x - 5/2)` ...[∵ रेखा का समीकरण है (y – y1) = m(x – x1]
⇒ 2y + 7 = 10x – 25
⇒ 10x – 2y – 32 = 0
⇒ 10x – 2y = 32
⇒ 5x – y = 16 ...(i)
अब, जांचें कि बिंदु A(2, 7) समीकरण (i) पर स्थित है या नहीं।
5 × 2 – 7
= 10 – 7
= 3 ≠ 16
अत:, बिंदु A(2, 7) रेखा खंड के लंब समद्विभाजक पर स्थित नहीं है।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित बिंदुओं को जोड़नेवाले रेखाखंड त्रिभुज बना सकते हैं क्या? यदि त्रिभुज बनता हो तो भुजाओं के आधार पर त्रिभुज का प्रकार लिखिए।
P(-2, -6), Q(-4, -2), R(-5, 0)
निम्नलिखित बिंदुओं को जोड़नेवाले रेखाखंड त्रिभुज बना सकते हैं क्या? यदि त्रिभुज बनता हो तो भुजाओं के आधार पर त्रिभुज का प्रकार लिखिए।
A(`sqrt2, sqrt2`), B(`-sqrt2 , -sqrt2`), C(`-sqrt6 , sqrt6`)
सिद्ध कीजिए, कि A(4, -1), B(6, 0), C(7, -2) और D(5, -3) वर्ग के शीर्ष बिंदु हैं।
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरी ज्ञात कीजिए:
(-5, 7), (-1, 3)
बिंदुओं A(0, 6) और B(0, –2) के बीच की दूरी ______ है।
यदि बिंदुओं Q(– 6, 5) और R(– 2, 3) को मिलाने वाले रेखाखंड का मध्य-बिंदु `P (a/3, 4)` है, तो a का मान ______ है।
बिंदुओं A(1, 5) और B(4, 6) को मिलाने वाले रेखाखंड का लंब समद्वि भाजक y-अक्ष को निम्नलिखित बिंदु पर काटता ______ हैं।
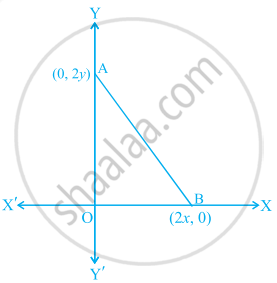
आकृति में दर्शाए गए त्रिभुज AOB के तीनों शीर्षो से समदूरस्थ बिंदु के निर्देशांक ______ हैं।
यदि (a, b), बिंदुओं A(10, –6) और B(k, 4) को मिलाने वाले रेखाखंड का मध्य-बिंदु है तथा a – 2b = 18 है, तो k का मान और दूरी AB ज्ञात कीजिए।
बिन्दु O(0, 0) तथा P(3, 4) के बीच की दूरी ज्ञात कीजिए।
