Advertisements
Advertisements
Question
बिंदु P(5, –3), बिंदुओं A(7, –2) और B(1, –5) को मिलाने वाले रेखाखंड को समत्रिभाजित करने वाले दो बिंदुओं में से एक बिंदु है।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण:
मान लीजिए P(5, –3) बिंदु A(7, –2) और B(1, –5) को मिलाने वाले रेखाखंड को आंतरिक रूप से k : 1 के अनुपात में विभाजित करता है।
खण्ड सूत्र के अनुसार बिन्दु P का निर्देशांक होगा
`((k(1) + (1)(7))/(k + 1), (k(-5) + 1(-2))/(k + 1))`
अर्थात, `((k+ 7)/(k + 1), (-5k - 2)/(k + 1))`
अब, (5, –3) = `((k + 7)/(k + 1), (-5k - 2)/(k + 1))`
⇒ `(k + 7)/(k + 1)` = 5
⇒ k + 7 = 5k + 5
⇒ – 4k = – 2
∴ k = `1/2`
तो बिंदु P रेखाखंड AB को 1 : 2 के अनुपात में विभाजित करता है।
अतः, AB के त्रिखंड बिंदु में बिंदु P है।
APPEARS IN
RELATED QUESTIONS
बिंदु P(– 4, 2), बिंदुओं A(– 4, 6) और B(– 4, – 6) को मिलाने वाले रेखाखंड पर स्थित हैं।
यदि P(9a, – 2, – b), बिंदुओं A(3a + 1, –3) और B(8a, 5) को मिलाने वाले रेखाखंड को 3 : 1 के अनुपात में विभाजित करे, तो a और b के मान ज्ञात कीजिए।
द्वितीय चतुर्थांश में स्थित किसी बिंदु के भुज और कोटि के क्रमशः चिह्न हैं :
बिंदु (–10, 0) स्थित है :
बिंदु (–5, 2) और (2, –5) स्थित हैं :
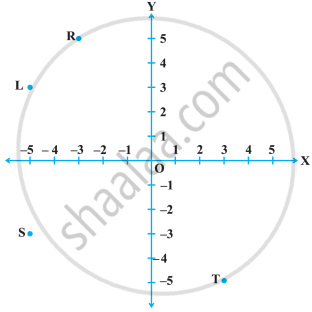
निम्नलिखित आकृति में, निर्देशांक (–5, 3) वाला बिंदु है :
y-अक्ष से बिंदु P(3, 4) की लांबिक दूरी है :
उस बिंदु के निर्देशांक, जिसकी कोटि `-1/2` और भुज 1 है, `-1/2, 1` होंगे।
उस बिंदु के निर्देशांक (2, 0) हैं जो y-अक्ष पर x-अक्ष से 2 मात्रक की दूरी पर स्थित है।
उस बिंदु के निर्देशांक ज्ञात कीजिए, जो जिसकी कोटि – 4 है और जो y-अक्ष पर स्थित है।
