Advertisements
Advertisements
प्रश्न
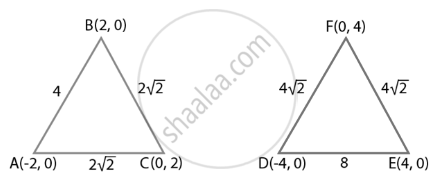
शीर्षों A(– 2, 0), B(2, 0) और C(0, 2) वाला त्रिभुज ABC शीर्षों D(–4, 0), E(4, 0) और F(0, 4) वाले त्रिभुज DEF के समरूप है।
विकल्प
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण:
दूरी के सूत्र का प्रयोग करके,
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
हम ढूंढ सकते हैं,
AB = `sqrt((2 + 2)^2 + 0) = sqrt(16)` = 4
BC = `sqrt((0 - 2)^2 + (2 - 0)^2) = sqrt(8) = 2sqrt(2)`
CA = `sqrt((-2 - 0)^2 + (0 - 2)^2) = sqrt(8) = 2sqrt(2)`
DE = `sqrt((4 + 4)^2 + 0) = sqrt(64)` = 8
EF = `sqrt((0 - 4)^2 + (4 - 0)^2) = sqrt(32) = 4sqrt(2)`
FD = `sqrt((-4 - 0)^2 + (0 - 4)^2) = sqrt(32) = 4sqrt(2)`
∴ `("AB")/("DE") = ("BC")/("EF") = ("CA")/("FD") = 1/2`
⇒ ΔABC ∼ ΔDEF
अतः, त्रिभुज ABC और DEF समरूप हैं।
APPEARS IN
संबंधित प्रश्न
यदि बिंदु L(x, 7) और M(1, 15) के बीच की दूरी 10 हो, तो x का मान ज्ञात कीजिए।
सिद्ध कीजिए कि, P(2, -2), Q(7, 3), R(11, -1) और S(6, -6) समांतर चर्तुभुज के शीर्षबिंदु है।
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरी ज्ञात कीजिए:
(2, 3), (4, 1)
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरी ज्ञात कीजिए:
(-5, 7), (-1, 3)
निर्धारित कीजिए कि क्या बिंदु (1, 5), (2, 3) और (-2, -11) संरेखी हैं।
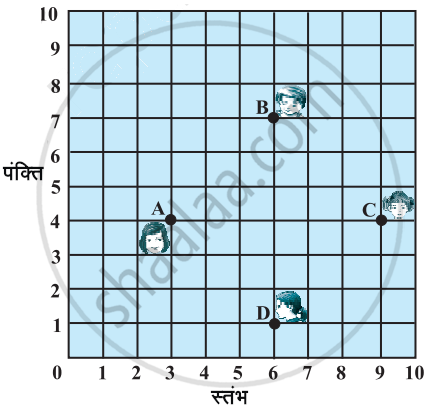
किसी कक्षा में, चार मित्र बिंदुओं A, B, C और D पर बैठे हुए हैं, जैसाकि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, 'क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?' चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें कौन सही है?
बिंदुओं (0, 5) और (–5, 0) के बीच की दूरी ______ है।
यदि बिंदु P(2, 1), बिंदुओं A(4, 2) और B(8, 4) को मिलाने वाले रेखाखंड पर स्थित तो ______ है।
बिंदु P(0, 2), बिंदुओं A(–1, 1 ) और B(3, 3) को मिलाने वाले रेखाखंड के लंब समद्विभाजक और y-अक्ष का प्रतिच्छेद बिंदु है।
बिंदु P(–2, 4), त्रिज्या 6 और केंद्र C(3, 5) वाले वृत्त पर स्थित है।
