Advertisements
Advertisements
Question
Two cells of emf E1, E2 and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure.

Deduce the expressions for
(1) the equivalent e.m.f of the combination
(2) the equivalent resistance of the combination, and
(3) the potential difference between the point A and B.
Solution
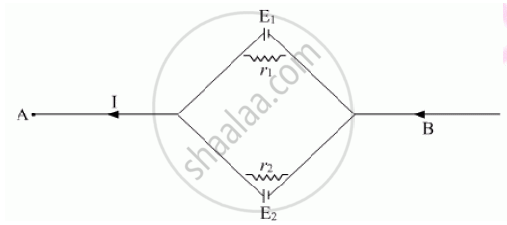
Let I1 and I2 be the current in two cells with emf E1 and E2 and internal resistance r1 and r2
So I = I1 + I2
Now let V be the potential difference between the points A and B. Since the first cell is connected between the points A and B.
V = potential difference across first cell
V = E1 − I1r1
`or I_1 =(E_1-V)/r_1`
Now, the second cell is also connected between the points A and B. So,
`or I_2 =(E_2-V)/r_2`
Thus, substituting for I1 and I2
`I =(E_1-V)/r_1 + (E_2-V)/r_2`
`or, I (E_1 /r_1 + E_2 /r_2)-V(1 /r_1 +1 /r_2)`
`V =((E_1r_2 + E_2r_1)/(r_1+r_2)) -I((r_1r_2)/(r_1 +r_2)) ..... (1)`
If E is effective e.m.f and r, the effective internal resistance of the parallel combination of the two cells then V = E − Ir …..(2)
Comparing (1) and (2)
`(1) E= (E_1r_2 + E_2r_1)/(r_1+r_2)`
This is equivalent e.m.f of the combination
`(2)r =(r_1r_2)/(r_1 +r_2)`
This is equivalent resistance of the combination.
(3) The potential difference between the point A and B is
V = E − Ir
RELATED QUESTIONS
Two cells of emfs 1.5 V and 2.0 V, having internal resistances 0.2 Ω and 0.3 Ω, respectively, are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
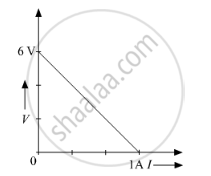
The plot of the variation of potential difference across a combination of three identical cells in series, versus current is shown below. What is the emf and internal resistance of each cell ?
Distinguish between emf and terminal voltage of a cell.
Six lead-acid types of secondary cells each of emf 2.0 V and internal resistance 0.015 Ω are joined in series to provide a supply to a resistance of 8.5 Ω. What are the current drawn from the supply and its terminal voltage?
A resistor R is connected to a cell of-emf e and internal resistance r. The potential difference across the resistor R is found to be V. State the relation between e, V, Rand r.
A cell of emf ‘E’ and internal resistance ‘r’ draws a current ‘I’. Write the relation between terminal voltage ‘V’ in terms of E, I and r ?
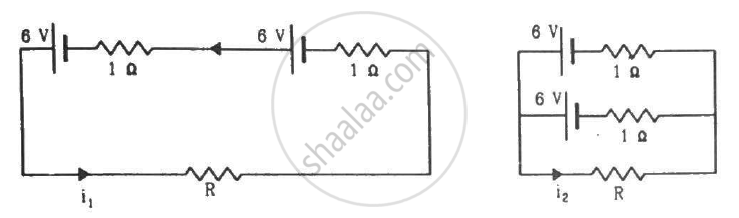
Find the value of i1/i2 in the following figure if (a) R = 0.1 Ω (b) R = 1 Ω and (c) R = 10 Ω. Note from your answers that in order to get more current from a combination of two batteries, they should be joined in parallel if the external resistance is small and in series if the external resistance is large, compared to the internal resistance.
Answer the following question.
A cell of emf E and internal resistance r is connected across a variable resistor R. Plot the shape of graphs showing a variation of terminal voltage V with (i) R and (ii) circuit current I.
Five cells each of emf E and internal resistance r send the same amount of current through an external resistance R whether the cells are connected in parallel or in series. Then the ratio `("R"/"r")` is:
