Advertisements
Advertisements
Question
Two charges q1 and q2 are placed at (0, 0, d) and (0, 0, – d) respectively. Find locus of points where the potential a zero.
Solution
Following the principle of superposition of potentials as
described in last section, let us find the potential V due to a collection of discrete point charges q1, q2, …, qn, at a point P.
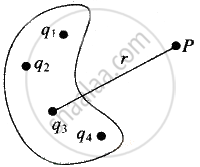
| The potential at P due to the system of point charges is given as the sum of their individual potentials at P, V = `1/(4piε_0) sum q_i/r_i` |
As we know, the potential at point P is V = `sumV_i`,
Where `V_i = q_i/(4piε_0) ; r_i` = magnitude of position vector P relative to qr
Then `V = 1/(4piε_0) sum q_i/r_"pi"`
Let us take a point on the required plane as (x, y, z). The two charges lies on z-axis at a separation of 2d. The potential at the point P due to two charge is given by
`q_1/(sqrt(x^2 + y^2 + (z - d)^2)) + q_2/(sqrt(x^2 + y^2 + (z + d)^2))` = 0
∴ `q_1/(sqrt(x^2 + y^2 + (z - d)^2)) = (-q_2)/(sqrt(x^2 + y^2 + (z + d)^2))`
On squaring and simplifying, we get
`x^2 + y^2 + z^2 + [((q_1/q_2)^2 + 1)/((q_1/q_2)^2 - 1)] (2zd) + d^2 - 0`
The standard equation of sphere is `x^2 + y^2 + z^2 + 2ux + 2uy + 2wz + g` = 0
With centre `(-u, -v, -w)` and radius `sqrt(u^2 + v^2 + w^2) - g`
Hence centre of sphere will be `(0, 0 - d[(q_1^2 + q_2^2)/(q_1^2 - q_2^2)])`
And radius is `r = sqrt((d[(q_1^2 + q_2^2)/(q_1^2 - q_2^2)])^2 - d^2) = (2q_1q_2d)/(q_1^2 - q_2^2)`
APPEARS IN
RELATED QUESTIONS
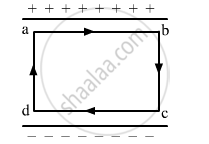
The electric field inside a parallel plate capacitor is E. Find the amount of work done in moving a charge q over a closed loop a b c d a.
Three capacitors each of capacitance 9 pF are connected in series.
- What is the total capacitance of the combination?
- What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Deduce an expression for equivalent capacitance C when three capacitors C1, C2 and C3 connected in parallel.
Figure 4 below shows a capacitor C, an inductor L and a resistor R, connected in series
to an a.c. supply of 220 V

Calculate:
1) The resonant frequency of the given CLR circuit.
2) Current flowing through·the circuit.
3) Average power consumed by the circuit.
Suppose a charge +Q1 is given to the positive plate and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
The plates of a capacitor are 2⋅00 cm apart. An electron-proton pair is released somewhere in the gap between the plates and it is found that the proton reaches the negative plate at the same time as the electron reaches the positive plate. At what distance from the negative plate was the pair released?
Three capacitors each of 4 µF are to be connected in such a way that the effective capacitance is 6µF. This can be done by connecting them:
Three different capacitors are·connected in series. Then:-
Capacitors connected in series have ______
Two equal capacitors are first connected in series and then in parallel The ratio of the equivalent capacities in the two cases will be ______.
