Advertisements
Advertisements
प्रश्न
Two charges q1 and q2 are placed at (0, 0, d) and (0, 0, – d) respectively. Find locus of points where the potential a zero.
उत्तर
Following the principle of superposition of potentials as
described in last section, let us find the potential V due to a collection of discrete point charges q1, q2, …, qn, at a point P.
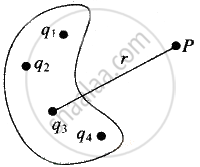
| The potential at P due to the system of point charges is given as the sum of their individual potentials at P, V = `1/(4piε_0) sum q_i/r_i` |
As we know, the potential at point P is V = `sumV_i`,
Where `V_i = q_i/(4piε_0) ; r_i` = magnitude of position vector P relative to qr
Then `V = 1/(4piε_0) sum q_i/r_"pi"`
Let us take a point on the required plane as (x, y, z). The two charges lies on z-axis at a separation of 2d. The potential at the point P due to two charge is given by
`q_1/(sqrt(x^2 + y^2 + (z - d)^2)) + q_2/(sqrt(x^2 + y^2 + (z + d)^2))` = 0
∴ `q_1/(sqrt(x^2 + y^2 + (z - d)^2)) = (-q_2)/(sqrt(x^2 + y^2 + (z + d)^2))`
On squaring and simplifying, we get
`x^2 + y^2 + z^2 + [((q_1/q_2)^2 + 1)/((q_1/q_2)^2 - 1)] (2zd) + d^2 - 0`
The standard equation of sphere is `x^2 + y^2 + z^2 + 2ux + 2uy + 2wz + g` = 0
With centre `(-u, -v, -w)` and radius `sqrt(u^2 + v^2 + w^2) - g`
Hence centre of sphere will be `(0, 0 - d[(q_1^2 + q_2^2)/(q_1^2 - q_2^2)])`
And radius is `r = sqrt((d[(q_1^2 + q_2^2)/(q_1^2 - q_2^2)])^2 - d^2) = (2q_1q_2d)/(q_1^2 - q_2^2)`
APPEARS IN
संबंधित प्रश्न
Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination.
An electrical technician requires a capacitance of 2 µF in a circuit across a potential difference of 1 kV. A large number of 1 µF capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
A circuit is set up by connecting inductance L = 100 mH, resistor R = 100 Ω and a capacitor of reactance 200 Ω in series. An alternating emf of \[150\sqrt{2}\] V, 500/π Hz is applies across this series combination. Calculate the power dissipated in the resistor.
A capacitor of capacitance 5⋅00 µF is charged to 24⋅0 V and another capacitor of capacitance 6⋅0 µF is charged to 12⋅0 V. (a) Find the energy stored in each capacitor. (b) The positive plate of the first capacitor is now connected to the negative plate of the second and vice versa. Find the new charges on the capacitors. (c) Find the loss of electrostatic energy during the process. (d) Where does this energy go?
Three capacitors of capacitance `C_1 = 3muf` , `C_2 = 6muf` , `C_3 = 10muf` , are connected to a 10V battery as shown in figure 3 below :
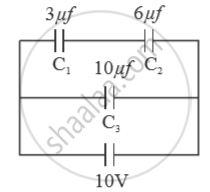
Calculate :
(a) Equivalent capacitance.
(b) Electrostatic potential energy stored in the system
An ac circuit consists of a series combination of circuit elements X and Y. The current is ahead of the voltage in phase by `pi /4` . If element X is a pure resistor of 100Ω ,
(a) name the circuit element Y.
(b) calculate the rms value of current, if rms value of voltage is 141V.
(c) what will happen if the ac source is replaced by a dc source ?
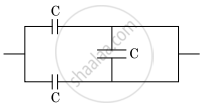
The equivalent capacitance of the combination shown in the figure is ______.
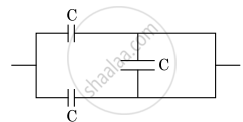
The equivalent capacitance of the combination shown in the figure is ______.
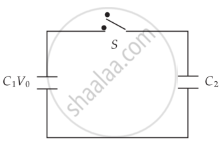
A capacitor of capacity C1 is charged to the potential of V0. On disconnecting with the battery, it is connected with an uncharged capacitor of capacity C2 as shown in the adjoining figure. Find the ratio of energies before and after the connection of switch S.