Advertisements
Advertisements
प्रश्न
Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination.
उत्तर
When the capacitors are connected in parallel,
Equivalent capacitance, CP=C1+C2
The energy stored in the combination of the capacitors, `E_P=1/2C_pV^2`
`=>E_P=1/2(C_1+C_2)(100^2)=0.25J`
⇒(C1+C2)=5×10−5 .....(i)
When the capacitors are connected in series,
Equivalent capacitance, `C_S=(C_1C_2)/(C_1+C_2)`
The energy stored in the combination of the capacitors,
`E_S=1/2C_SV^2`
`=>E_S=1/2(C_1C_2)/(C_1+C_2)(100)^2=0.045J`
`1/2(C_1C_2)/(5xx10^(-5))(100)^2=0.045J`
⇒C1C2=0.045×10−4×5×10−5×2=4.5×10−10
(C1−C2)2=(C1+C2)2−4C1C2
⇒(C1−C2)2=25×10−10−4×4.5×10−10=7×10−10
`=>(C_1-C_2)=sqrt(7xx10^(-10))=2.64xx10^(-5)`
C1−C2=2.64×10−5 .....(ii)
Solving (i) and (ii), we get
C1 = 35 μF and C2 = 15 μF
When the capacitors are connected in parallel, the charge on each of them can be obtained as follows:
Q1=C1V=35×10−6×100=35×10−4 C
Q2=C2V=15×10−6×100=15×10−4 C
APPEARS IN
संबंधित प्रश्न
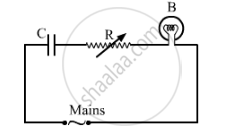
A capacitor 'C', a variable resistor 'R' and a bulb 'B' are connected in series to the ac mains in circuit as shown. The bulb glows with some brightness. How will the glow of the bulb change if (i) a dielectric slab is introduced between the plates of the capacitor, keeping resistance R to be the same; (ii) the resistance R is increased keeping the same capacitance?
Deduce an expression for equivalent capacitance C when three capacitors C1, C2 and C3 connected in parallel.
Figure 4 below shows a capacitor C, an inductor L and a resistor R, connected in series
to an a.c. supply of 220 V

Calculate:
1) The resonant frequency of the given CLR circuit.
2) Current flowing through·the circuit.
3) Average power consumed by the circuit.
The plates of a parallel-plate capacitor are given equal positive charges. What will be the potential difference between the plates? What will be the charges on the facing surfaces and on the outer surfaces?
A parallel-plate capacitor having plate area 25 cm2 and separation 1⋅00 mm is connected to a battery of 6⋅0 V. Calculate the charge flown through the battery. How much work has been done by the battery during the process?
The plates of a capacitor are 2⋅00 cm apart. An electron-proton pair is released somewhere in the gap between the plates and it is found that the proton reaches the negative plate at the same time as the electron reaches the positive plate. At what distance from the negative plate was the pair released?
A capacitor of capacitance 5⋅00 µF is charged to 24⋅0 V and another capacitor of capacitance 6⋅0 µF is charged to 12⋅0 V. (a) Find the energy stored in each capacitor. (b) The positive plate of the first capacitor is now connected to the negative plate of the second and vice versa. Find the new charges on the capacitors. (c) Find the loss of electrostatic energy during the process. (d) Where does this energy go?
Capacitors connected in series have ______
Two charges q1 and q2 are placed at (0, 0, d) and (0, 0, – d) respectively. Find locus of points where the potential a zero.
