Advertisements
Advertisements
प्रश्न
Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination.
उत्तर
When the capacitors are connected in parallel,
Equivalent capacitance, CP=C1+C2
The energy stored in the combination of the capacitors, `E_P=1/2C_pV^2`
`=>E_P=1/2(C_1+C_2)(100^2)=0.25J`
⇒(C1+C2)=5×10−5 .....(i)
When the capacitors are connected in series,
Equivalent capacitance, `C_S=(C_1C_2)/(C_1+C_2)`
The energy stored in the combination of the capacitors,
`E_S=1/2C_SV^2`
`=>E_S=1/2(C_1C_2)/(C_1+C_2)(100)^2=0.045J`
`1/2(C_1C_2)/(5xx10^(-5))(100)^2=0.045J`
⇒C1C2=0.045×10−4×5×10−5×2=4.5×10−10
(C1−C2)2=(C1+C2)2−4C1C2
⇒(C1−C2)2=25×10−10−4×4.5×10−10=7×10−10
`=>(C_1-C_2)=sqrt(7xx10^(-10))=2.64xx10^(-5)`
C1−C2=2.64×10−5 .....(ii)
Solving (i) and (ii), we get
C1 = 35 μF and C2 = 15 μF
When the capacitors are connected in parallel, the charge on each of them can be obtained as follows:
Q1=C1V=35×10−6×100=35×10−4 C
Q2=C2V=15×10−6×100=15×10−4 C
APPEARS IN
संबंधित प्रश्न
Suppose a charge +Q1 is given to the positive plate and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
The following figure shows two capacitors connected in series and joined to a battery. The graph shows the variation in potential as one moves from left to right on the branch containing the capacitors.
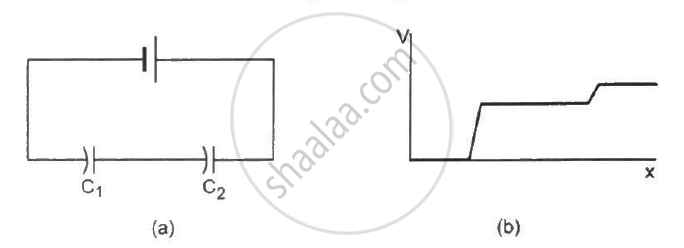
Each plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a batter. Now,
(a) the facing surfaces of the capacitor have equal and opposite charges
(b) the two plates of the capacitor have equal and opposite charges
(c) the battery supplies equal and opposite charges to the two plates
(d) the outer surfaces of the plates have equal charges
The separation between the plates of a charged parallel-plate capacitor is increased. Which of the following quantities will change?
(a) Charge on the capacitor
(b) Potential difference across the capacitor
(c) Energy of the capacitor
(d) Energy density between the plates
A parallel-plate capacitor is connected to a battery. A metal sheet of negligible thickness is placed between the plates. The sheet remains parallel to the plates of the capacitor.
An ac circuit consists of a series combination of circuit elements X and Y. The current is ahead of the voltage in phase by `pi /4` . If element X is a pure resistor of 100Ω ,
(a) name the circuit element Y.
(b) calculate the rms value of current, if rms value of voltage is 141V.
(c) what will happen if the ac source is replaced by a dc source ?
An ac circuit consists of a series combination of circuit elements X and Y. The current is ahead of the voltage in phase by `pi/4`. If element X is a pure resistor of 100 Ω,
(a) name the circuit element Y.
(b) calculate the rms value of current, if rms of voltage is 141 V.
(c) what will happen if the ac source is replaced by a dc source
Two parallel plate capacitors X and Y, have the same area of plates and same separation between plates. X has air and Y with dielectric of constant 2, between its plates. They are connected in series to a battery of 12 V. The ratio of electrostatic energy stored in X and Y is ______.
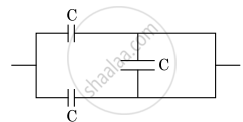
The equivalent capacitance of the combination shown in the figure is ______.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel. What is the total capacitance of the combination?
