Advertisements
Advertisements
Question
Two dice are numbered 1, 2, 3, 4, 5, 6 and 1, 1, 2, 2, 3, 3, respectively. They are thrown and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9 separately.
Solution
Number of total outcomes = 36
(i) Let E1 = Event of getting sum 2 = {(1, 1), (1, 1)}
∴ n(E1) = 2
∴ `P(E_1) = (n(E_1))/(n(S)) = 2/36 = 1/8`
(ii) Let E2 = Event of getting sum 3 = {(1, 2), (1, 2), (2, 1), (2, 1)}
∴ n(E2) = 4
∴ `P(E_2) = (n(E_2))/(n(S)) = 4/36 = 1/9`
(iii) Let E3 = Event of getting sum 4 = {(2, 2), (2, 2), (3, 1), (3, 1), (1, 3), (1, 3)}
∴ n(E3) = 6
∴ `P(E_3) = (n(E_3))/(n(S)) = 6/36 = 1/6`
(iv) Let E4 = Event of getting sum 5 = {(2, 3), (2, 3), (4, 1), (4, 1), (3, 2), (3, 2)}
∴ n(E4) = 6
∴ `P(E_4) = (n(E_4))/(n(S)) = 6/36 = 1/6`
(v) Let E5 = Event of getting sum 6 = {(3, 3), (3, 3), (4, 2), (4, 2), (5, 1), (5, 1)}
∴ n(E5) = 6
∴ `P(E_5) = (n(E_5))/(n(S)) = 6/36 = 1/6`
(vi) Let E6 = Event of getting sum 7 = {(4, 3), (4, 3), (5, 2), (5, 2), (6, 1), (6, 1)}
∴ n(E6) = 6
∴ `P(E_6) = (n(E_6))/(n(S)) = 6/36 = 1/6`
(vii) Let E7 = Event of getting sum 8 = {(5, 3), (5, 3), (6, 2), (6, 2)}
∴ n(E7) = 4
∴ `P(E_7) = (n(E_7))/(n(S)) = 4/36 = 1/9`
(viii) Let E8 = Event of getting sum 9 = {(6, 3), (6, 3)}
∴ n(E8) = 2
∴ `P(E_8) = (n(E_8))/(n(S)) = 2/36 = 1/18`
APPEARS IN
RELATED QUESTIONS
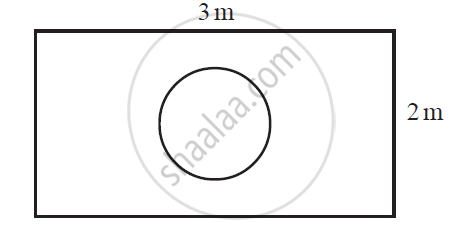
Suppose you drop a die at random on the rectangular region shown in the given figure. What is the probability that it will land inside the circle with diameter 1m?
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is black and a king
In a class, there are 18 girls and 16 boys. The class teacher wants to choose one pupil for class monitor. What she does, she writes the name of each pupil on a card and puts them into a basket and mixes thoroughly. A child is asked to pick one card from the basket. What is the probability that the name written on the card is the name of a boy?
From a pack of 52 playing cards, all cards whose numbers are multiples of 3 are removed. A card is now drawn at random. What is the probability that the card drawn is an even numbered red card?
How many possibilities is following?
Select one card from the pack of 52 cards.
There are six cards in a box, each bearing a number from 0 to 5. Find the probability of the following event, that a card drawn show, a whole number.
A die is rolled twice. Find the probability that 5 will come up both the times.
Which of the following cannot be the probability of an event?
Cards with numbers 2 to 101 are placed in a box. A card is selected at random. Find the probability that the card has a square number
One card is drawn at random from a well-shuffled deck of 52 playing cards. What is the probability of getting a black king?
