Question

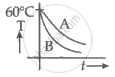
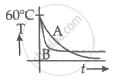
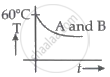
Two identical beakers A and B contain equal volumes of two different liquids at 60°C each and is left to cool down. Liquid in A has a density of 8 × 10² kg/m³ and specific heat of 2000 J kg^-1 K^-1 while the liquid in B has a density of 10³ kg m^-3 and specific heat of 4000 J kg^-1 K^-1. Which of the following best describes their temperature versus time graph schematically? (assume the emissivity of both the beakers to be the same.)

Options

• 

• 

• 

• 

Answer 1

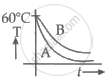
Explanation:

Given: T = 60°C is the initial temperature of both beakers A and B.

The liquid volume in both beakers is the same,

V = V_A = V_B

The liquid density in beaker A is

ρ_A = 8 × 10² kg/m³

The liquid density in beaker B is

ρ_B = 10³ kg/m³,

Beaker A's liquid-specific heat is

S_A = 2000 J kg^-1 k^-1,

Beaker B's liquid-specific heat is

S_B = `4000J/(kg.K)`

To find: Select the appropriate cooling graph for both liquids.

Cooling law of Newton: 

`(dQ)/(dt) = h/(ms)(T - T_0)`

= `h/(Vrhos)(T - T_0)`

In the equation above, `(dQ)/(dt)` stands for the rate of cooling, h for the heat transfer coefficient, m = V_ρ for the mass of the liquid, s for its specific heat, T for its temperature, T₀ for its environment, V for volume, and ρ for its density.

h, V, T, and T₀ are constants for both liquids in beakers A and B:

`(dQ_A)/(dt) ∝ 1/(rho_AS_A); (dQ_B)/(dt) ∝ 1/(rho_sS_B)` .......(i)

Add the supplied values to the equation (i),

`(dQ_A)/(dt) ∝ 1/(800 xx 2000);`

`(dQ_A)/(dt) ∝ 6.25 xx 10^-7` .....(ii)

As shown by equations (ii) and (iii),

`(dQ_A)/(dt) > (dQ_B)/(dt)`

for the duration of cooling.

Hence, as illustrated in option b, graph B will always be above graph A.