Advertisements
Advertisements
Question
Two identical circular coils, P and Q each of radius R, carrying currents 1 A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.
Solution

Magentic field at the centre of the coil are perpendicular to each other. Therefore net magnetic field (B) is the resultant of the two fields caused due to coil P and Q, respectively.
`B_P = (μ_oI)/(2πR)= (μ_o)/(2πR)`
`B_Q= (μ_oI)/(2πR)= (μ_osqrt3)/(2πR)`
Net magnetic field, `B = sqrt(B_P^2 + B_Q^2)`
`=sqrt((μ_o/(2πR))^2 + ( (μ_osqrt3)/(2πR))^2) `
`= μ_o/(2πR)sqrt4`
`= μ_o/(πR)`
For direction of net magnetic field
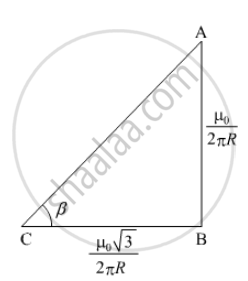
`tanβ =(AB)/(BC)`
`= (μ_o/(2πR))/((μ_osqrt3)/(2πR)) = 1/sqrt3`
`β= 30^@`
The direction of net magnetic field is 30° with the X-direction.
RELATED QUESTIONS
A circular loop is kept in that vertical plane which contains the north-south direction. It carries a current that is towards north at the topmost point. Let A be a point on the axis of the circle to the east of it and B a point on this axis to the west of it. The magnetic field due to the loop
A circular loop of radius R carries a current I. Another circular loop of radius r(<<R) carries a current i and is placed at the centre of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
A piece of wire carrying a current of 6.00 A is bent in the form of a circular are of radius 10.0 cm, and it subtends an angle of 120° at the centre. Find the magnetic field B due to this piece of wire at the centre.
A circular coil of 200 turns has a radius of 10 cm and carries a current of 2.0 A. (a) Find the magnitude of the magnetic field \[\vec{B}\] at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?
The magnetic field at a distance r from a long wire carrying current I is 0.4 tesla. The magnetic field at a distance 2 r is ______.
If we double the radius of a coil keeping the current through it unchanged, then the magnetic field at any point at a large distance from the centre becomes approximately.
A small square loop of wire of side l is placed inside a large square loop of side L (L >> l). The loop is coplanar and their centers coincide. The mutual inductance of the system is proportional to is
An electron is projected along the axis of a circular conductor carrying some current. Electron ______
Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line intergral
`ℑ(L ) = |int_(-L)^L B.dl|` taken along z-axis.
- Show that ℑ(L) monotonically increases with L.
- Use an appropriate Amperian loop to show that ℑ(∞) = µ0I, where I is the current in the wire.
- Verify directly the above result.
- Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about ℑ(L) and ℑ(∞)?
