Question

Use Huygens' principle to show the propagation of a plane wavefront from a denser medium to a rarer medium. Hence find the ratio of the speeds of wavefronts in the two media.

Answer 1

 

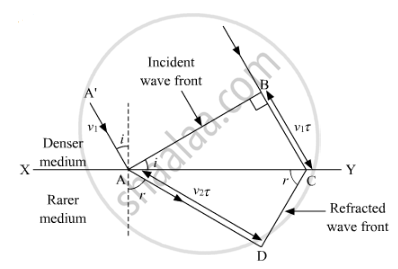
Let XY be the surface separating the denser medium and the rarer medium.
Let:
v₁ = Speed of light wave in the denser medium
v₂ = Speed of light wave in the rarer medium
Let us consider a plane wavefront AB propagating in the direction AA'. Let this wavefront incident on the interface at an angle of incidence i with the normal to the interface.
Let τ be the time taken by the wavefront to travel the distance BC in denser medium.

⇒BC=v1τ

 To determine the shape of refracted wavefront, we will draw a sphere of radius v₂τ from point A in the rarer medium. Let CD represent a tangent plane drawn from point C onto the sphere. 
Now,
AD=v2τ

Here, CD would represent the refracted wavefront. Considering the triangles ABC and ADC, we get

`sini=(BC)/(AC)=(v_1τ)/(AC)`

` sinr=(AD)/(AC)=(v_2τ)/(AC)`

⇒sini/sinr=v_1/v-2   .....(1)

where
 i = Angle of incidence 
 r = Angle of refraction

Since r > i (rays bend away from the normal on travelling from denser to rarer medium), the speed of light in the rarer medium (v₂) will be greater than the speed of light in the denser medium (v₁).
If c represents the speed of light in vacuum, then

`μ1=c/v_1`

` μ2=c/v_2`

where
μ₁ = Refractive index of denser medium ​
μ₂ = Refractive index of rarer medium 

Further, (1) can be written as

`μ1sini=μ2sinr`

This is the Snell's law of refraction.

Now, if λ₁ and λ₂ represent the wavelengths of light in the denser medium and rarer medium, respectively, and if the distance BC is λ₁, then the distance AD will be λ₂. So, we have

`λ_1/λ_2=(BC)/(AD)=v_1/v_2`

`⇒v_1/v_2=λ_1/λ_2`