Advertisements
Advertisements
Question
Two identical circular loops 1 and 2 of radius R each have linear charge densities −λ and +λ C/m respectively. The loops are placed coaxially with their centres `Rsqrt3` distance apart. Find the magnitude and direction of the net electric field at the centre of loop 1.
Solution
Magnitude of electric field at any point on the axis of a uniformly charged loop is given by,
`E=λ/(2∈_0) (rR)/(r^2+R^2)^(3/2) .....(i)`
where
R = Radius of the loop
r = Position of the point from the centre of the loop
λ = Linear charge density of the loop
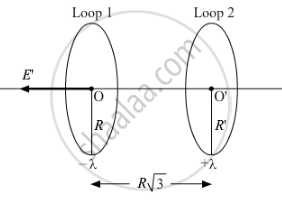
Electric field at the centre of loop 1 due to charge present on it is zero. [ From (i), when r = 0 ]
`| vecE_1 | = 0 (As Z = 0)`
Electric field at a point outside the loop 2 on the axis passing normally is
`|vecE_2| = [lambdaR]/(2ε_0) . [Z]/[R^2 + Z^2]^(3/2)`
Since, Z = `Rsqrt3`
= `[lambdaR]/(2ε_0) . [Rsqrt3]/[(R^2 + 3R^2)^(3/2)]`
= `[lambdasqrt3]/[16ε_0R]` twowards right (As λ is positive)
So, net electric field at the centre of loop 1
`vecE = vecE_1 + vecE_2`
= 0 + `[lambdasqrt3]/[16ε_0R] = [lambdasqrt3]/[16ε_0R]`
This is the net electric field at the centre of loop 1 due to the charge on both the loops. The direction of this net field is from loop 2 to loop 1 as shown in the above figure.
APPEARS IN
RELATED QUESTIONS
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
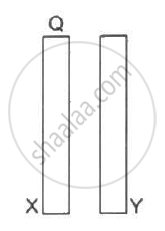
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
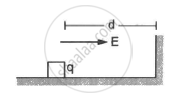
A block of mass containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any), find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
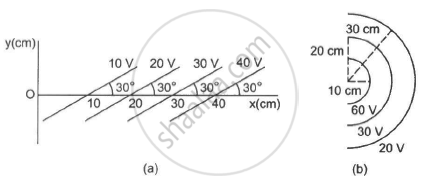
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
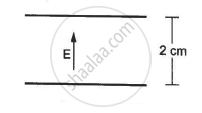
An electric field of magnitude 1000 NC−1 is produced between two parallel plates with a separation of 2.0 cm, as shown in the figure. (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower place in the direction of the field, so that it may reach the upper plate? (c) Suppose the electron is projected from the lower place with the speed calculated in part (b). The direction of projection makes an angle of 60° with the field. Find the maximum height reached by the electron.
Draw equipotential surfaces corresponding to a uniform electric field in the z-directions.
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
Electric field at a point is defined as ______.
