Advertisements
Advertisements
प्रश्न
Two identical circular loops 1 and 2 of radius R each have linear charge densities −λ and +λ C/m respectively. The loops are placed coaxially with their centres `Rsqrt3` distance apart. Find the magnitude and direction of the net electric field at the centre of loop 1.
उत्तर
Magnitude of electric field at any point on the axis of a uniformly charged loop is given by,
`E=λ/(2∈_0) (rR)/(r^2+R^2)^(3/2) .....(i)`
where
R = Radius of the loop
r = Position of the point from the centre of the loop
λ = Linear charge density of the loop
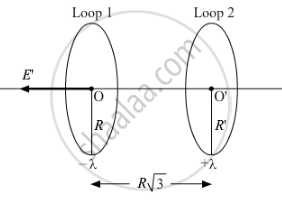
Electric field at the centre of loop 1 due to charge present on it is zero. [ From (i), when r = 0 ]
`| vecE_1 | = 0 (As Z = 0)`
Electric field at a point outside the loop 2 on the axis passing normally is
`|vecE_2| = [lambdaR]/(2ε_0) . [Z]/[R^2 + Z^2]^(3/2)`
Since, Z = `Rsqrt3`
= `[lambdaR]/(2ε_0) . [Rsqrt3]/[(R^2 + 3R^2)^(3/2)]`
= `[lambdasqrt3]/[16ε_0R]` twowards right (As λ is positive)
So, net electric field at the centre of loop 1
`vecE = vecE_1 + vecE_2`
= 0 + `[lambdasqrt3]/[16ε_0R] = [lambdasqrt3]/[16ε_0R]`
This is the net electric field at the centre of loop 1 due to the charge on both the loops. The direction of this net field is from loop 2 to loop 1 as shown in the above figure.
APPEARS IN
संबंधित प्रश्न
Plot a graph showing the variation of resistivity of a conductor with temperature.
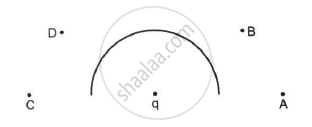
In the following figure shows a charge q placed at the centre of a hemisphere. A second charge Q is placed at one of the positions A, B, C and D. In which position(s) of this second charge, the flux of the electric field through the hemisphere remains unchanged?
(a) A
(b) B
(c) C
(d) D
A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and outer surfaces? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
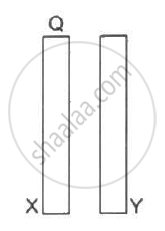
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
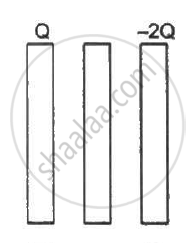
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
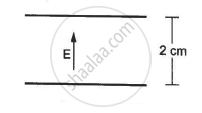
An electric field of magnitude 1000 NC−1 is produced between two parallel plates with a separation of 2.0 cm, as shown in the figure. (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower place in the direction of the field, so that it may reach the upper plate? (c) Suppose the electron is projected from the lower place with the speed calculated in part (b). The direction of projection makes an angle of 60° with the field. Find the maximum height reached by the electron.
Electric field at a point is defined as ______.
