Advertisements
Advertisements
Question
Use the real number line to find the range of values of x for which:
x < 0 and –3 ≤ x < 1
Solution
x < 0 and –3 ≤ x < 1
Both the given in equations are true in the range where their graphs on the real number lines overlap.
The graphs of the given in equations can be drawn as:
x < 0
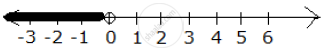
–3 ≤ x < 1

From both graphs, it is clear that their common range is –3 ≤ x < 0
APPEARS IN
RELATED QUESTIONS
Solve the following inequation and represent the solution set on the number line:
4x - 19 < (3x)/5 - 2 <= (-2)/5 + x, x ∈ R
Represent the following inequalities on real number line:
– 4 < x < 4
Find the set of values of x, satisfying:
`7x + 3 >= 3x - 5` and `x/4 - 5 <= 5/4 -x`, where x ∈ N
Graph the solution set for each inequality:
-3< x <5
Solve 2 ≤ 2x – 3 ≤ 5, x ∈ R and mark it on number line.
Solve the inequation : `-2(1)/(2) + 2x ≤ (4x)/(3) ≤ (4)/(3) + 2x, x ∈ "W"`. Graph the solution set on the number line.
Solve the given inequation and graph the solution on the number line : 2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
Find the range of values of a, which satisfy 7 ≤ – 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.
Solve the following inequation, write the solution set and represent it on the real number line.
`5x - 21 < (5x)/7 - 6 ≤ -3 3/7 + x, x ∈ R`
The solution set for the following number line is:

