Advertisements
Advertisements
Question
Using energy conservation, along a vertical circular motion controlled by gravity, prove that the difference between the extreme tensions (or normal forces) depends only upon the weight of the objects.
Solution
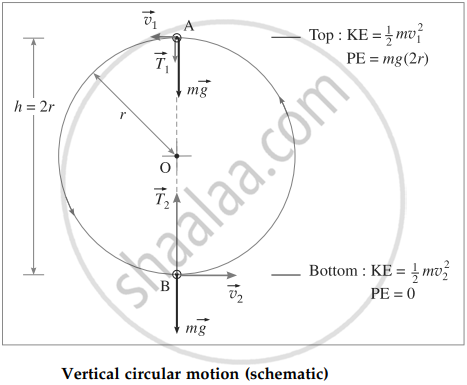
Consider a small body (or particle) of mass m tied to a string and revolved in a vertical circle of radius r at a place where the acceleration due to gravity is g. At every instant of its motion, the body is acted upon by two forces, namely, its weight `vec"mg"` and the tension `vec"T"` in the string.
Let `"v"_2` be the speed of the body and `"T"_2` be the tension in the string at the lowest point B. We take the reference level for zero potential energy to be the bottom of the circle. Then, the body has only kinetic energy `1/2"mv"_2^2` at the lowest point.
∴ `"T"_2 = "mv"_2^2/"r" + "mg"` ...(1)
and the total energy at the bottom = KE + PE
`= 1/2"mv"_2^2 + 0`
`= 1/2 "mv"_2^2` ...(2)
Let v1 be the speed and T1 the tension in the string at the highest point A. As the body goes from B to A, it rises through a height h = 2r.
∴ `"T"_1 = "mv"_1^2/"r" - "mg"` .....(3)
and the total energy at A = KE + PE
`= 1/2 "mv"_1^2 + "mg"(2r)` ...(4)
Then, from Eqs. (1) and (3),
`"T"_2 - "T"_1 = "mv"_2^2/"r" + "mg" - ("mv"_1^2/"r" - "mg")`
`= "m"/"r" ("v"_2^2 - "v"_1^2) + 2 "mg"` ...(5)
Assuming that the total energy of the body is conserved, the total energy at the bottom = total energy at the top
Then, from Eqs. (2) and (4),
`1/2 "mv"_2^2 = 1/2"mv"_1^2 + "mg"(2r)`
∴ `"v"_2^2 - "v"_1^2 = 4 "gr"` ...(6)
Substituting this in Eq. (5),
`"T"_2 - "T"_1 = "m"/"r" (4 "gr") + 2 "mg"`
`= 4 "mg" + 2 "mg"`
= 6 mg
Therefore, the difference in the tensions in the string at the highest and the lowest points is 6 times the weight of the body.
APPEARS IN
RELATED QUESTIONS
Answer in Brief:
Part of a racing track is to be designed for curvature of 72m. We are not recommending the vehicles to drive faster than 216 kmph. With what angle should the road be tilted? By what height will its outer edge be, with respect to the inner edge if the track is 10 m wide?
A road is constructed as per the given requirements. The coefficient of static friction between the tyres of a vehicle on this road is 0.8, will there be any lower speed limit? By how much can the upper speed limit exceed in this case?
(Given: r = 72 m, vo = 216 km/h, w = 10 m, θ = 78°4', h = 9.805 m)
During a stunt, a cyclist (considered to be a particle) is undertaking horizontal circles inside a cylindrical well of radius 6.05 m. If the necessary friction coefficient is 0.5, how much minimum speed should the stunt artist maintain? The mass of the artist is 50 kg. If she/he increases the speed by 20%, how much will the force of friction be?
Using the energy conservation, derive the expressions for the minimum speeds at different locations along a vertical circular motion controlled by gravity. Is zero speed possible at the uppermost point? Under what condition/s?
A block of mass m is moving on rough horizontal surface with momentum p. The coefficient of friction between the block and surface is µ. The distance covered by the block before it stops is [g =acceleration due to gravity)
A vehicle of mass m is moving with momentum p on a rough horizontal road. The coefficient of friction between the tyres and the horizontal road is µ. The stopping distance is ____________.
(g = acceleration due to gravity)
A cyclist with combined mass 80 kg goes around a curved road with a uniform speed 20 m/s. He has to bend inward by an angle `theta` = tan-1 (0.50) with the vertical. The force of friction acting at the point of contact of tyres and road surface is______.
[g = 10 m/s2 ]
A horizontal circular platform of mass 100 kg is rotating at 5 r.p.m. about vertical axis passing through its centre. A child of mass 20 kg is standing on the edge of platform. If the child comes to the centre of platform then the frequency of rotation will become ______.
A body of mass 10 kg is attached to a wire 0.3 m long. Its breaking stress is 4.8 × 107 N/m2. The area of cross-section of the wire is 10-6m2. The maximum angular velocity with which it can be rotated 111 a horizontal circle is ______.
In the case of conical pendulum, if T is the tension in the string and θ is the semivertical angle of cone, then the component of tension which balances the centrifugal force in equilibrium position is ______.
In the case of conical pendulum, if 'T' is the tension in the string and 'θ' is the semi-vertical angle of cone, then the component which provides necessary centripetal force is ______.
A particle executes uniform circular motion with angular momentum 'L'. Its rotational kinetic energy becomes half when the angular frequency is doubled. Its new angular momentum is ______.
If friction is made zero for a road, can a vehicle move safely on this road?
What is banking of a road?
Why it is necessary banking of a road?
A curved road 5 m wide is to be designed with a radius of curvature 900 m. What should be the elevation of the outer edge of the road above the inner edge optimum speed of the vehicles rounding the curve is 30 m/s.
The centripetal acceleration of the bob of a conical pendulum is, in the usual notation, ______.
A cyclist is undertaking horizontal circles inside a cylindrical well of radius 5 m. If the friction coefficient is 0.5, what should be the minimum speed of the cyclist?
Write about the kinetic friction between the road and the tyres.
A body performing uniform circular motion has ______.
A horizontal force of 0.5 N is required to move a metal plate of area 10−2 m2 with a velocity of 3 × 10−2m/s, when it rests on 0.5 × 10−3 m thick layer of glycerin. Find the coefficient of viscosity of glycerin.
