Advertisements
Advertisements
Question
Using Huygens’ principle, verify the laws of reflection at a plane surface.
Solution
Verification of Laws of Reflection using Huygens Principle

Consider any point Q on the incident wavefront PA.
When the disturbance from P on incident wavefront reaches point P', the disturbance from point Q reaches Q'
If c is the velocity of light, then the time taken by light to go from point Q to Q' (via point K) is given by,
`t = (QK)/c + (KQ')/c `....(i)
In right-angled ΔAQK,
∠QAK = i
∴ QK = AK sin i
In right-angled ΔKQ'P'
∠Q'P'K = r
`:. KQ' = KP' sin r`
Substituting these values in equation (1),
`t = (AK sin i)/c + (KP'sin r)/c`
`t = (AK sin i + (AP' - AK)sin r)/c` (∵ KP' = AP' - AK)
`t = (AP' sin r + AK(sin i - sin r))/c` ...(ii)
The rays from different points on incident wavefront will take the same time to reach the corresponding points on the reflected wavefront if ‘t’ given by equation (ii) is independent of AK
∴ AK (sin i − sin r) = 0
sin i − sin r = 0
sin i = sin r
i = r
i.e the angle of incidence is equal to the angle of reflection
Also, the incident ray (LA or MP'), reflected ray (AA'L' or P'M'), and the normal (AN) − all lie in the same plane.
APPEARS IN
RELATED QUESTIONS
Using Huygens's construction of secondary wavelets explain how a diffraction pattern is obtained on a screen due to a narrow slit on which a monochromatic beam of light is incident normally.
The refractive indices of water and diamond are `4/3` and 2.42 respectively. Find the speed of light in water and diamond. (c = 3x108 m/s)
Use Huygens’s principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light.
Define the term wavefront. Using Huygen’s wave theory, verify the law of reflection.
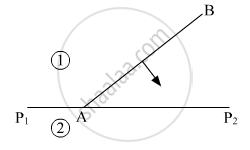
Define the term 'wavefront of light'. A plane wavefront AB propagating from a denser medium (1) into a rarer medium (2) is incident of the surface P1P2 separating the two media as shown in fig.
Using Huygen's principle, draw the secondary wavelets and obtain the refracted wavefront in the diagram.
According to Huygen's construction, relation between old and new wavefront is ______.
What is the geometrical shape of the wavefront for:
- Light diverging from a point source?
- The pattern of wavefront of the light from a distant star intercepted by earth?
How is a wavefront different from a ray?
Using Huygen's wave theory of light, show that the angle of incidence is equal to the angle of reflection. Draw a neat and labelled diagram.
What type of wavefronts are associated with a point source of light?
