Advertisements
Advertisements
Question
What are the two methods for obtaining coherent sources in the laboratory?
Solution
In the laboratory, coherent sources can be obtained by using (1) Lloyd's mirror and (2) Fresnel's biprism.
- Lloyd's mirror:
This is an extensively used device. The light from a source is made to fall at a grazing angle on a plane mirror as shown in figure.
Some of the light falls directly on the screen as shown by the blue lines in the figure and some light falls after reflection, as shown by the red lines. The reflected light appears to come from a virtual source and so we get two sources. They are derived from a single source and hence are coherent. They interfere and an interference pattern is obtained as shown in the figure. Note that even though we have shown the direct and reflected rays by blue and red lines, the light is monochromatic having a single wavelength. - Fresnel's biprism:
A biprism is a prism with a vertex angle of nearly 180°. It can be considered to be made up of two prisms with very small refracting angle ranging from 30′ to 1°, joined at their bases. In experimental arrangement, the refracting edge of the biprism is kept parallel to the length of the slit. Monochromatic light from a source is made to pass through a narrow slit S as shown in Figure and fall on the biprism.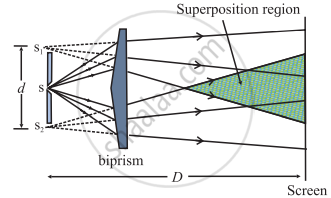
The two halves of the biprism form virtual images S1 and S2. These are coherent sources having obtained from a single secondary source S. The two waves coming from S1 and S2 interfere and form interference fringes like that in Young’s double-slit experiment in the shaded region shown in the figure.
APPEARS IN
RELATED QUESTIONS
Laser light of wavelength 630 nm is incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits, calculate:
1) fringe separation i.e. fringe width.
2) distance of 10th bright fringe from the centre of the interference pattern
The intensity at the central maximum (O) in a Young’s double slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would equal `(I_0)/4`.

The intensity of the light coming from one of the slits in Young's experiment is twice the intensity of the light coming from the other slit. What will be the approximate ratio of the intensities of the bright and dark fringes in the resulting interference pattern?
Draw a neat labelled ray diagram of the Fresnel Biprism experiment showing the region of interference.
What is intensity (or) amplitude division?
How do source and images behave as coherent sources?
Obtain the equation for resultant intensity due to interference of light.
Explain Young’s double-slit experimental setup and obtain the equation for path difference.
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
In Young's double-slit experiment, if the width of the 2nd bright fringe is 4 x 10-2 cm, then the width of the 4th bright fringe will be ______ cm.
A graph is plotted between the fringe-width Z and the distance D between the slit and eye-piece, keeping other adjustment same. The correct graph is
A.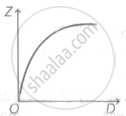 |
B. |
C.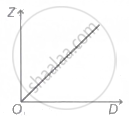 |
D.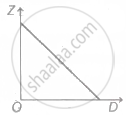 |
The distance between the first and ninth bright fringes formed in a biprism experiment is ______.
(`lambda` = 6000 A, D = 1.0 m, d = 1.2 mm)
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
In a Young's experiment, two coherent sources are placed 0.60 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 1 mm from the central fringe, the wavelength of monochromatic light used would be ____________.
Two sources of light 0.5 mm apart are placed at a distance of 2.4 m and wavelength of light is 5000 Å. The phase difference between the two light waves interfering on the screen at a point at a distance 3 mm from central bright band is ____________.
In interference experiment, intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at (sin30° = cos60° = 0.5, `lambda` = wavelength of light, d = slit width) ____________.
If two waves represented by `"y"_1 = 3 "sin" omega "t"` and `"y"_2 = 5 "sin" (omega "t" + pi/3)` interfere at a point, then the amplitude of the resulting wave will be about ____________.
In a biprism experiment, the slit separation is 1 mm. Using monochromatic light of wavelength 5000 Å, an interference pattern is obtained on the screen. Where should the screen be moved? so that the change in fringe width is 12.5 x 105 m?
In the biprism experiment, the fringe width is 0.4 mm. What is the distance between the 4th dark band and the 6th bright band on the same side?
Waves from two coherent sources of light having an intensity ratio I1 : I2 equal to 'x' interfere. Then in the interference pattern obtained on the screen, the value of (Imax - Imin)/(Imax + Imin) is ______
In the biprism experiment, a source of monochromatic light is used for a certain distance between slit and eyepiece. When the distance between two virtual sources is changed from dA to dB, then the fringe width is changed from ZA to ZB. The ratio ZA to ZB is ______
Light waves from two coherent sources arrive at two points on a screen with a path difference of zero and λ/2. The ratio of the intensities at the points is ______
In an interference experiment, the intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at ____________.
(cos 60° = 0.5, `lambda` = wavelength of light, d = slit width)
White light is passed through a double slit and interference is observed on a screen 1.5 m away. The separation between the slits is 0.3 mm. The first violet and red fringes are formed 2.0 mm and 3.5 mm away from the central white fringes. The difference in wavelengths of red and violet light is ______ nm.
Two coherent sources P and Q produce interference at point A on the screen where there is a dark band which is formed between 4th bright band and 5th bright band. Wavelength of light used is 6000 Å. The path difference between PA and QA is ______.
The path difference between two interference light waves meeting at a point on the screen is `(87/2)lambda`. The band obtained at that point is ______.
