Advertisements
Advertisements
Question
What is the sum of an odd numbers between 1 to 50?
Solution
The odd numbers between 1 to 50 are
1, 3, 5, ......, 49
The above sequence is an A.P.
∴ a = 1
∴ d = 5 – 3 = 2
Let the number of terms in the A.P. be n.
Then, tn = 49
Since tn = a + (n – 1)d,
49 = 1 + (n – 1)(2)
∴ 49 = 1 + 2n – 2
∴ 49 = 2n - 1
∴ 49 + 1 = 2n
∴ n =`50/2`
∴ n = 25
Now, Sn = `"n"/2 ("t"_1 + "t"_"n")`
∴ S25 = `25/2 (1 + 49)`
= 12.5 × 50
= 625
∴ The sum of odd numbers between 1 to 50 is 625.
APPEARS IN
RELATED QUESTIONS
How many terms of the A.P. 27, 24, 21, .... should be taken so that their sum is zero?
If the mth term of an A.P. is 1/n and the nth term is 1/m, show that the sum of mn terms is (mn + 1)
The sum of the first p, q, r terms of an A.P. are a, b, c respectively. Show that `\frac { a }{ p } (q – r) + \frac { b }{ q } (r – p) + \frac { c }{ r } (p – q) = 0`
In an AP given an = 4, d = 2, Sn = −14, find n and a.
Find the sum of first 15 multiples of 8.
Find the sum of the odd numbers between 0 and 50.
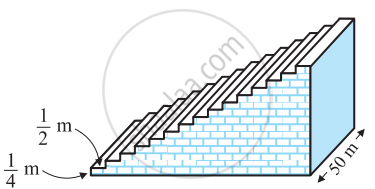
A small terrace at a football field comprises 15 steps, each of which is 50 m long and built of solid concrete. Each step has a rise of `1/4` m and a tread of `1/2` m (See figure). Calculate the total volume of concrete required to build the terrace.
[Hint: Volume of concrete required to build the first step = `1/4 xx 1/2 xx 50 m^3`]
If the 12th term of an A.P. is −13 and the sum of the first four terms is 24, what is the sum of first 10 terms?
Which term of the AP 3,8, 13,18,…. Will be 55 more than its 20th term?
Find the common difference of an AP whose first term is 5 and the sum of its first four terms is half the sum of the next four terms.
The 9th term of an A.P. is 449 and 449th term is 9. The term which is equal to zero is
Two A.P.'s have the same common difference. The first term of one of these is 8 and that of the other is 3. The difference between their 30th term is
Let the four terms of the AP be a − 3d, a − d, a + d and a + 3d. find A.P.
The term A.P is 8, 10, 12, 14,...., 126 . find A.P.
Find the sum of first 10 terms of the A.P.
4 + 6 + 8 + .............
How many terms of the A.P. 25, 22, 19, … are needed to give the sum 116 ? Also find the last term.
In an A.P. a = 2 and d = 3, then find S12
How many terms of the AP: –15, –13, –11,... are needed to make the sum –55? Explain the reason for double answer.
Find the sum of those integers from 1 to 500 which are multiples of 2 as well as of 5.
