Question

When two thin lenses of focal lengths f₁ and f₂ are kept coaxially and in contact, prove that their combined focal length ‘f’ is given by: `1/f = 1/f_1 + 1/f_2`

Answer 1

Let two thin lenses L₁ and L₂ of focal lengths f₁ and f₂ be put in contact. O is a point object at a distance u from the lens L₁ Its image is formed at I after refraction through the two lenses at a distance v from the combination. The lens L₁ forms the image of O at I’. I’, then serves as a virtual object for the lens L₂ which forms a real image at I.

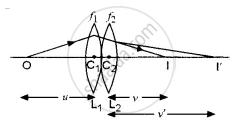
Now, we know that by lens formula
`1/v - 1/u = 1/f`

Applying this relation for refraction at the lens
L₁ of focal length f1 can be written as

`1/v' - 1/u = 1/f_1`    ...(i)

For refraction at the lens L₂
u = v', v = v

∴ For this lens `1/v - 1/v' = 1/f_2`    ...(ii)

And if F is the focal length of the combination, then

`1/v - 1/u = 1/F`

Adding (i) and (ii), we get

`1/v' - 1/u + 1/v - 1/v' = 1/f_1  + 1/f_2`

or `1/v -1/u = 1/f_1  + 1/f_2`

or `1/"F" = 1/f_1  + 1/f_2 `