Advertisements
Advertisements
Question
Show that the time period of revolution of particles in a cyclotron is independent of their speeds. Why is this property necessary for the operation of a cyclotron?
Solution
Let a particle of charge q and mass m enter a region of magnetic field B with a velocity v normal to the field. The particle follows a circular path inside the cyclotron, and the necessary centripetal force is provided by the magnetic field.
Therefore, we have
`qvB=(mv^2)/r`
`:.r=(mv^2)/(qvB)=(mv)/(qB)`
Now, the time period of revolution will be
`T=d/v=(2pir)/v=(2pimv)/(qBv)=(2pim)/(qB)`
Therefore, from the above expression, we see that the time period is independent of the speed of the particle.
The time period should be independent of speed so that the frequency of revolution of the particle remains equal to the frequency of the ac source applied to the cyclotron.
APPEARS IN
RELATED QUESTIONS
State the underlying principle of a cyclotron. Write briefly how this machine is used to accelerate charged particles to high energies
Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
If a watch-glass containing a small quantity of water is placed on two dissimilar magnetic poles, then water ______.
An α-particle and a proton are released from the centre of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency?
Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the does?
An electron is projected horizontally with a kinetic energy of 10 keV. A magnetic field of strength 1.0 × 10−7 T exists in the vertically upward direction.
(a) Will the electron deflect towards the right or left of its motion?
(b) Calculate the sideways deflection of the electron while travelling through 1 m. Make appropriate approximations.
Figure shows a rod PQ of length 20.0 cm and mass 200 g suspended through a fixed point O by two threads of lengths 20.0 cm each. A magnetic field of strength 0.500 T exists in the vicinity of the wire PQ, as shown in the figure. The wires connecting PQ with the battery are loose and exert no force on PQ. (a) Find the tension in the threads when the switch S is open. (b) A current of 2.0 A is established when the switch S is closed. Find the tension in the threads now.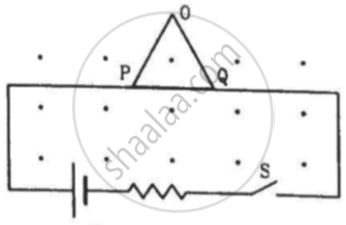
Cyclotron frequency of a charged particle having charge q and mass m in a cyclotron producing magnetic field B is ______.
Assertion: The frequency of circular motion of a charged particle in cyclotron is independent of the mass of the particle.
Reason: Greater the mass of the particle less will be the frequency of the particle.
A cyclotron can accelerate ______.
Verify that the cyclotron frequency ω = eB/m has the correct dimensions of [T]–1.
