Advertisements
Advertisements
Question
Two identical cells of emf 1.5 V each joined in parallel, supply energy to an external circuit consisting of two resistances of 7 Ω each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
Solution
The two cells are connected in parallel. So, the equivalent emf is 1.5 V.
Now, the two resistors are connected in parallel. So, the equivalent resistance is
`1/R_(eq)=1/R+1/R=2/R`
`:.R_(eq)=R/2=7/2=3.5Omega`
The terminal voltage of the cells measured by the voltmeter is 1.4 V.
The net internal resistance of the combination of cells is
`r_(eq)=((varepsilon-V)/V)R`
`:.r_(eq)=(1.5-1.4)/1.4xx3.5=0.1/1.4xx3.5=0.25 Omega`
Now, the individual internal resistors are connected in parallel. So, the individual internal resistances is
`r_(eq)=(r')/2`
∴ r' = 2req = 2 x 0.25 = 0.5Ω
APPEARS IN
RELATED QUESTIONS
Two cells of emfs 1.5 V and 2.0 V, having internal resistances 0.2 Ω and 0.3 Ω, respectively, are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
The plot of the variation of potential difference across a combination of three identical cells in series, versus current is shown below. What is the emf and internal resistance of each cell ?
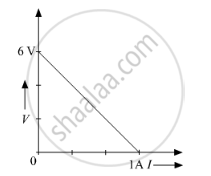
A cell of emf 'E' and internal resistance 'r' is connected across a variable load resistor R. Draw the plots of the terminal voltage V versus (i) R and (ii) the current I.
It is found that when R = 4 Ω, the current is 1 A and when R is increased to 9 Ω, the current reduces to 0.5 A. Find the values of the emf E and internal resistance r.
Nichrome and copper wires of same length and same radius are connected in series. Current I is passed through them. Which wire gets heated up more? Justify your answer.
The equivalent resistance between points. a and f of the network shown in Figure 2 is :
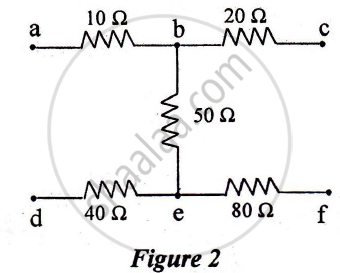
a) 24 Ω
b) 110 Ω
c) 140 Ω
d) 200 Ω
A cell of emf ‘E’ and internal resistance ‘r’ draws a current ‘I’. Write the relation between terminal voltage ‘V’ in terms of E, I and r ?
Two non-ideal batteries are connected in series. Consider the following statements:-
(A) The equivalent emf is larger than either of the two emfs.
(B) The equivalent internal resistance is smaller than either of the two internal resistances.
How many time constants will elapse before the power delivered by a battery drops to half of its maximum value in an RC circuit?
Answer the following question.
A cell of emf E and internal resistance r is connected across a variable resistor R. Plot the shape of graphs showing a variation of terminal voltage V with (i) R and (ii) circuit current I.
An ac generator generates an emf which is given by e = 311 sin (240 πt) V. Calculate:
- frequency of the emf.
- r.m.s. value of the emf.
