Advertisements
Advertisements
Question
Find the electric field intensity due to a uniformly charged spherical shell at a point (i) outside the shell. Plot the graph of electric field with distance from the centre of the shell.
Solution
Let σ be the uniform surface charge density of a thin spherical shell of radius R
Field outside the shell: Consider a point P outside the shell with radius vector r.

To calculate E at P, we take the Gaussian surface to be a sphere of radius r with centre O passing through P. All the points on this sphere are equivalent relative to the given charged configuration.
Therefore, the electric field at each point of the Gaussian surface has the same magnitude E and is along the radius vector at each point.
Thus, E and ΔS at every point are parallel, and the flux through each element is E ΔS. Summing over entire ΔS, the flux through the Gaussian surface is E × 4πr2. The charge enclosed is σ × 4πR2.
By Gauss’s law, we get
`Exx4pir^2=sigma/epsilon_0xx4piR^2`
`:.E=(sigmaR^2)/(epsilon_0r^2)=q/(4piepsilon_0r^2)`
Where q = 4πR2σ is the total charge on the spherical shell.
The electric field is directed outward if q > 0 and inward if q < 0. This however is exactly the field produced by a charge q placed at the centre O. Thus, for points outside the shell, the field caused by a uniformly charged shell is as if the entire charge of the shell is concentrated at its centre.
APPEARS IN
RELATED QUESTIONS
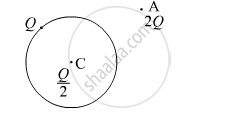
A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge`Q/2` is placed at its centre C and an other charge +2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find (i) the force on the charge at the centre of shell and at the point A, (ii) the electric flux through the shell.
Using Gauss's law in electrostatics, deduce an expression for electric field intensity due to a uniformly charged infinite plane sheet. If another identical sheet is placed parallel to it, show that there is no electric field in the region between the two sheets ?
A small conducting sphere of radius 'r' carrying a charge +q is surrounded by a large concentric conducting shell of radius Ron which a charge +Q is placed. Using Gauss's law, derive the expressions for the electric field at a point 'x'
(i) between the sphere and the shell (r < x < R),
(ii) outside the spherical shell.
Using Gauss’ law deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point
(i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R.
(r being the distance from the centre of the shell)
Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
How is the field directed if (i) the sheet is positively charged, (ii) negatively charged?
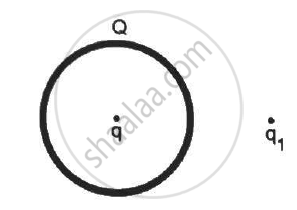
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure . All the three charges are positive. The force on the charge at the centre is ____________.
A spherical volume contains a uniformly distributed charge of density 2.0 × 10 -4 Cm-3 Find the electric field at a point inside the volume at a distance 4⋅0 cm from the centre.
