Advertisements
Advertisements
Question
An ac generator generates an emf which is given by e = 311 sin (240 πt) V. Calculate:
- frequency of the emf.
- r.m.s. value of the emf.
Solution
(1) Given that
e = 311 sin (240 πt) V ...(i)
∵ e = e0 sin (ωt) V ...(ii)
From equations (i) and (ii)
e0 = 311 and ωt = 240 πt
∴ ω = 240 π
f = `omega/(2pi)`
`= (240 pi)/(2pi)`
= 120 cycle/s
e0 = Peak emf of the generator = 33
∵ Peak emf = rms · emf × `sqrt2`
∴ rms = `1/sqrt2` peak emf
= 0.707 × 311 = 219.87 volts
∴ rms = 219.87 volts
(2) Given the number of turns in the primary winding is NP = 60 turns.
The number of turns in secondary winding is NS = 3000 turns.
APPEARS IN
RELATED QUESTIONS
Two cells of emfs 1.5 V and 2.0 V, having internal resistances 0.2 Ω and 0.3 Ω, respectively, are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9 Ω is used in the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell.
Two cells of emf E1, E2 and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure.

Deduce the expressions for
(1) the equivalent e.m.f of the combination
(2) the equivalent resistance of the combination, and
(3) the potential difference between the point A and B.
The temperatures of the junctions of a bismuth-silver thermocouple are maintained at 0°C and 0.001°C. Find the thermo-emf (Seebeck emf) developed. For bismuth-silver, a = − 46 × 10−6 V°C−1 and b = −0.48 × 10−6 V°C−2.
Two cells of emfs approximately 5 V and 10 V are to be accurately compared using a potentiometer of length 400 cm.
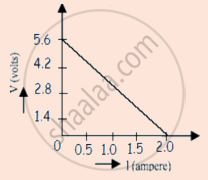
A straight line plot showing the terminal potential difference (V) of a cell as a function of current (I) drawn from it, is shown in the figure. The internal resistance of the cell would be then ______.
A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of P.D. across R, versus R.
A block of metal is heated directly by dissipating power in the internal resistance of block. Because of temperature rise, the resistance increases exponentially with time and is given by R(t) = 0.5 e2t, where t is in second. The block is connected across a 110 V source and dissipates 7644 J heat energy over a certain period of time. This period of time is ______ × 10-1 sec (take ln 0.367 = -1).
