Advertisements
Advertisements
Question
Will the angular momentum of a planet be conserved? Justify your answer.
Solution
The torque experienced by the Earth due to the gravitational force of the Sun is given by,
`vecτ = vec"r" xx vec"F" = vec"r" xx (-("GM"_"S""M"_"E")/"r"^2 hat"r") = 0`
Since `vec"r" = "r", hat"r", (hat"r" xx hat"r") = 0`
So `vecτ = ("d" vec"L")/"dt" = 0`
It implies that angular momentum `vec"L"` is a constant vector. Hence L is conserved.
APPEARS IN
RELATED QUESTIONS
If the masses of the Earth and Sun suddenly double, the gravitational force between them will ___________.
If the distance between the Earth and Sun were to be doubled from its present value, the number of days in a year would be ___________.
The work done by the Sun’s gravitational force on the Earth is __________.
If the mass and radius of the Earth are both doubled, then the acceleration due to gravity g'
Define gravitational potential energy.
Derive the expression for gravitational potential energy.
Prove that at points near the surface of the Earth, the gravitational potential energy of the object is U = mgh.
If a comet suddenly hits the Moon and imparts energy which is more than the total energy of the Moon, what will happen?
If the ratio of the orbital distance of two planets `"d"_1/"d"_2` = 2, what is the ratio of gravitational field experienced by these two planets?
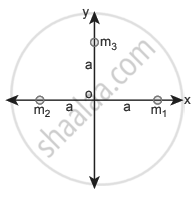
Calculate the gravitational field at point O due to three masses m1, m2 and m3 whose positions are given by the following figure. If the masses m1 and m2 are equal what is the change in a gravitational field at the point O?