Advertisements
Advertisements
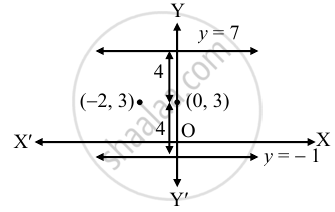
Question
Write the equation of the line: parallel to the X-axis and at a distance of 4 units from the point (−2, 3).
Solution
Equation of a line parallel to the X-axis is of the form y = k (k > 0 or k < 0).
Since, the line is at a distance of 4 units from the point (−2, 3).
∴ k = 3 + 4 = 7 or k = 3 − 4 = −1
∴ The equation of the required line is y = 7 or y = −1.
APPEARS IN
RELATED QUESTIONS
Write the equation of the line: parallel to the X-axis and at a distance of 5 units from it and above it.
Write the equation of the line: parallel to the Y-axis and at a distance of 5 units from it and to the left of it.
Obtain the equation of the line: parallel to the X-axis and making an intercept of 3 units on the Y-axis.
Obtain the equation of the line containing the point: B(4, – 3) and parallel to the X-axis.
Show that the lines x – 2y – 7 = 0 and 2x − 4y + 5 = 0 are parallel to each other.
If the line 3x + 4y = p makes a triangle of area 24 square units with the co-ordinate axes, then find the value of p.
Find the co-ordinates of the circumcentre of the triangle whose vertices are A(– 2, 3), B(6, – 1), C(4, 3).
Find the distance of the point A(– 2, 3) from the line 12x – 5y – 13 = 0.
Find the distance between parallel lines 9x + 6y − 7 = 0 and 9x + 6y − 32 = 0.
Find the equation of the line passing through the point of intersection of lines x + y – 2 = 0 and 2x – 3y + 4 = 0 and making intercept 3 on the X-axis.
Which of the following lines passes through the origin?
Obtain the equation of the line which is parallel to the Y-axis and 2 units to the left of it.
Obtain the equation of the line which is parallel to the X-axis and making an intercept of 5 on the Y-axis.
Obtain the equation of the line which is: parallel to the Y-axis and making an intercept of 3 on the X-axis.
Obtain the equation of the line containing the point: (2, 3) and parallel to the X−axis.
