Advertisements
Advertisements
Question
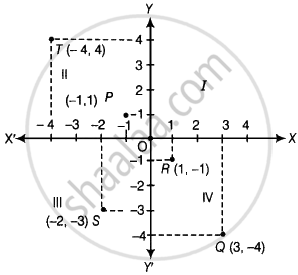
यदि बिंदुओं P(–1, 1), Q(3, –4), R(1, –1), S(–2, –3) और T(–4, 4) को आलेख कागज पर आलेखित किया जाए, तो चौथे चतुर्थांश के बिंदु हैं :
Options
P और T
Q और R
केवल S
P और R
Solution
Q और R
स्पष्टीकरण -
बिंदु P(–1, 1) में, x-निर्देशांक –1 इकाई है और y-निर्देशांक 1 इकाई है, इसलिए यह दूसरे चतुर्थांश में स्थित है।
इसी प्रकार, हम सभी बिंदुओं Q(3, –4), R(1, –1), S(–2, –3) और T(–4, 4) को आलेखित कर सकते हैं।
ग्राफ से यह स्पष्ट है कि बिंदु R और Q चौथे चतुर्थांश में स्थित हैं।
APPEARS IN
RELATED QUESTIONS
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। AD पर स्थित उस बिंदु P के निर्देशांक ज्ञात कीजिए, जिससे AP : PD = 2 : 1 हो।
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। माध्यिकाओं BE और CF पर स्थित क्रमश : ऐसे बिंदुओं Q और R के निर्देशांक ज्ञात कीजिए कि BQ : QE = 2 : 1 और CR : RF = 2 : 1 हो।
बिंदु (-3, 5) स्थित है : ______
यदि किसी बिंदु P की x-अक्ष से लांबिक दूरी 5 मात्रक हो तथा इस लंब का पाद x-अक्ष की ऋणात्मक दिशा पर स्थित हो, तो बिंदु P का ______
बिंदुओं O(0, 0), A(3, 0), B(3, 4), C(0, 4) को आलेखित करके तथा OA, AB, BC और CO को मिलाने पर, निम्नलिखित में से कौन-सी आकृति प्राप्त होगी?
यदि दो बिंदुओं P और Q के निर्देशांक क्रमश : (–2, 3) और (–3, 5) हैं तो (P का भुज) – (Q का भुज) बराबर है :
यदि P(5, 1), Q(8, 0), R(0, 4), S(0, 5) और O(0, 0) को एक आलेख कागज पर आलेखित किया जाए, तो x-अक्ष पर स्थित बिंदु हैं :
किसी बिंदु का भुज धनात्मक होता है :
उस बिंदु के निर्देशांक (2, 0) हैं जो y-अक्ष पर x-अक्ष से 2 मात्रक की दूरी पर स्थित है।
निम्नलिखित सारणी से प्राप्त बिंदुओं (x, y) को आलेखित कीजिए :
| x | 2 | 4 | – 3 | – 2 | 3 | 0 |
| y | 4 | 2 | 0 | 5 | – 3 | 0 |
