Advertisements
Advertisements
Question
यदि एक वृत्त PXAQBY की एक जीवा AB का लंब समद्विभाजक वृत्त को P और Q बिंदुओं पर प्रतिच्छेद करता है, तो सिद्ध कीजिए कि चाप PXA ≅ चाप PYB हैं।
Solution
मान लीजिए AB उस वृत्त की जीवा है जिसका केंद्र OPQ है, जीवा AB का लम्ब समद्विभाजक है, जो M पर प्रतिच्छेद करती है और यह सदैव O से होकर जाती है।
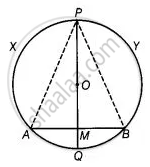
सिद्ध करना है - चाप PXA ≅ चाप PYB
रचना - AP और BP को मिलाइए।
प्रमाण - ΔAPM और ΔBPM में,
AM = MB ...[∵ PM, AB को समद्विभाजित करता है।]
∠PMA = ∠PMB ...[प्रत्येक 90°, ∵ PM ⊥ AB]
PM = PM ...[सामान्य]
∴ ΔAPM ∴ ΔBPM ...[SAS सर्वांगसमता द्वारा]
∴ PA = PB ...[C.P.C.T. द्वारा]
⇒ चाप PXA ≅ चाप PYB
APPEARS IN
RELATED QUESTIONS
वृत्त का केन्द्र वृत्त के ______ में स्थित है।
एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के _________ स्थित होता है।
वृत्त की सबसे बड़ी जीवा वृत्त का _____ होता है।
एक चाप _______ होता है, जब इसके सिरे एक व्यास के सिरे हों।
संलग्न आकृति देखकर लिखिए:
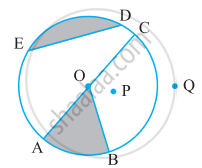
तीन त्रिज्याएँ
संलग्न आकृति देखकर लिखिए:

एक व्यास
क्या वृत का प्रत्येक जीवा उसका एक व्यास भी होती है?
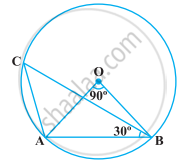
निम्नलिखित आकृति में, ∠AOB = 90° और ∠ABC = 30° है। तब, ∠CAO बराबर है :
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
त्रिभुज के सभी शीर्षबिंदुओं से जाने वाले वृत्त को क्या कहते हैं?
