Advertisements
Advertisements
Question
यह ज्ञात है कि वायु का घनत्व ρ ऊँचाई y (मीटरों में) के साथ इस संबंध के अनुसार घटता है:
ρ = ρ0e-y/y0
यहाँ समुद्र तल पर वायु का घनत्व ρ0 = 1.25 kg m-3 तथा y0 एक नियतांक है। घनत्व में इस परिवर्तन को वायुमंडल का नियम कहते हैं। यह संकल्पना करते हुए कि वायुमण्डल का ताप नियत रहता है (समतापी अवस्था) इस नियम को प्राप्त कीजिए। यह भी मानिए कि g का मान नियत रहता है।
Solution
समुद्र तल से ऊँचाई पर वायु के एक काल्पनिक बेलन पर विचार कीजिए जिसका अनुप्रस्थ क्षेत्रफल A है। माना बेलन की ऊँचाई dy है। बेलन के निचले तथा ऊपर वाले सिरों पर वायु दाब क्रमशः P तथा P + dP हैं।
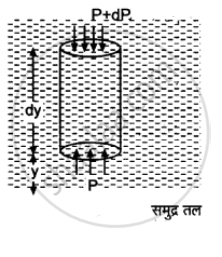
माना इस स्थान पर वायु का घनत्व ρ है।
तब बेलन का भार = द्रव्यमान × g
= A × dy × ρ × g
द्रव के बेलन के निचे वाले तथा ऊपर वाले सिरों पर ऊर्ध्वाधर बल क्रमशः PA तथा (P + dP) A है।
∴ बेलन संतुलन की स्थिति में है ; अतः अधोमुखी तथा ऊपरिमुखी बल बराबर होंगे।
∴ PA = Adyρg + (P + dP)A
⇒ -A dP = Aρgdy
या - dP = ρgdy ...(1)
∵ वातावरण का ताप स्थिर है ; अतः समतापी पराक्रम हेतु
PV = नियतांक या `"P""m"/rho = "K"_1 [∵ "V" = "m"/rho]`
`=> "P"/rho = "K"` ...[जहाँ K = K1/m]
या P = Kρ ∴ dP = K dρ
dP का मान समीकरण (1) में रखने पर,
-K dρ = ρgdy या `- ("d"rho)/rho = "g"/"K" "dy"`
समाकलन करने पर, `- "log" rho = "g"/"K""y" + "C"` ...(2)
जहाँ C समाकल स्थिरांक है।
परन्तु समुद्र तल पर y = 0 तथा ρ = ρ0 (दिया है)
∴ ` - "log" rho_0 = "g"/"K" * 0 + "C" => "C" = - "log" rho_0`
समीकरण (2) में C का मान रखने पर,
`"log" rho - "log" rho_0 = - "g"/"K" "y"`
या `"log"(rho/rho_0) = "y"/("K"//"g")`
`"K"/"g" = "y"_0` रखने पर,
`"log"(rho/rho_0) = - "y"/"y"_0 => rho/rho_0 = "e"^(-"y"//"y"_0)`
`rho = rho_0"e"^(-"y"//"y"_0)`
APPEARS IN
RELATED QUESTIONS
समुद्र तट से दूर कोई ऊर्ध्वाधर संरचना 109 Pa के अधिकतम प्रतिबल को सहन करने के लिए बनाई गई है। क्या यह संरचना किसी महासागर के भीतर किसी तेल कूप के शिखर पर रखे जाने के लिए उपयुक्त है? महासागर की गहराई लगभग 3km है। समुद्री धाराओं की उपेक्षा कीजिए।
1.0 m2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागों में बाँटा गया है। विभाजक दीवार के नीचे 20 cm2 क्षेत्रफल का कब्जेदार दरवाजा है। टैंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है। दोनों भाग 4.0 m ऊँचाई तक भरे गए हैं। दरवाजे को बंद रखने के लिए आवश्यक बल परिकलित कीजिए।
दो पात्रों के आधारों के क्षेत्रफल समान हैं परंतु आकृतियाँ भिन्न-भिन्न हैं। पहले पात्र में दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है। क्या दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान है। यदि ऐसा है तो भार मापने की मशीन पर रखे एक ही ऊँचाई तक जल से भरे दोनों पात्रों के पाठ्यांक भिन्न-भिन्न क्यों होते हैं?
रुधिर-आधान के समय किसी शिरा में, जहाँ दाब 2000 Pa है, एक सुई धँसाई जाती है। रुधिर के पात्र को किस ऊँचाई पर रखा जाना चाहिए ताकि शिरा में रक्त ठीक-ठीक प्रवेश कर सके। (संपूर्ण रुधिर का घनत्व = 1.06 × 103 kg m-3)
