Advertisements
Chapters
2: Estimation
3: Numbers in India and International System (With Comparison)
4: Place Value
5: Natural Numbers and Whole Numbers (Including Patterns)
6: Negative Numbers and Integers
7: Number Line
8: HCF and LCM
9: Playing with Numbers
10: Sets
11: Ratio
12: Proportion (Including Word Problems)
13: Unitary Method
14: Fractions
15: Decimal Fractions
16: Percent (Percentage)
17: Idea of Speed, Distance and Time
18: Fundamental Concepts of algebra
19: Fundamental Operations (Related to Algebraic Expressions)
20: Substitution (Including Use of Brackets as Grouping Symbols)
21: Framing Algebraic Expressions (Including Evaluation)
22: Simple (Linear) Equations (Including Word Problems)
▶ 23: Fundamental Concepts geometry
24: Angles (With their Types)
25: Properties of Angles and Lines (Including Parallel Lines)
26: Triangles (Including Types, Properties and Constructions)
27: Quadrilateral
28: Polygons
29: The Circle
30: Revision Exercise Symmetry (Including Constructions on Symmetry)
31: Recognition of Solids
32: Perimeter and Area of Plane Figures
33: Data Handling (Including Pictograph and Bar Graph)
34: Mean and Median
![Selina solutions for Mathematics [English] Class 6 chapter 23 - Fundamental Concepts geometry Selina solutions for Mathematics [English] Class 6 chapter 23 - Fundamental Concepts geometry - Shaalaa.com](/images/mathematics-english-class-6_6:44f3c4f6e33345f4bf41a86d406bf37f.jpg)
Advertisements
Solutions for Chapter 23: Fundamental Concepts geometry
Below listed, you can find solutions for Chapter 23 of CISCE Selina for Mathematics [English] Class 6.
Selina solutions for Mathematics [English] Class 6 23 Fundamental Concepts geometry Exercise 23 (A)
State, true or false, if false, correct the statement.
A dot has width but no length.
True
False
State, true or false, if false, correct the statement.
A ray has an infinite length only on one side of it.
True
False
State, true or false, if false, correct the statement.
A line segment PQ is written as \[\overleftrightarrow{PQ}\]
True
False
State, true or false, if false, correct the statement.
\[\overleftrightarrow{PQ}\] represents a straight line.
True
False
State, true or false, if false, correct the statement.
Three points are said to be collinear, if they lie in the same plane.
True
False
State, true or false, if false, correct the statement.
Three or more points all lying in the same line, are called collinear points.
True
False
Write how many line can be drawn through a given point?
Write how many line can be drawn through two given fixed points?
Write how many line can be drawn through three collinear points?
Write how many line can be drawn through three non-collinear points?
The shaded region of the given figure shows a plane:
(i) Name the three collinear points.
(ii) Name the three non-collinear points.
(iii) Name a pair of intersecting lines.
The shaded region of the given figure shows a plane:
State whether true or false of the following statement:
(i) Line DE is contained in the given plane P.
(ii) Lines AB and DE intersect at point C.
(iii) Points D, B and C are collinear.
(iv) Points D, B and E are collinear.
Correct the statement, if it is wrong:
A ray can be extended infinitely on either side.
Correct
Incorrect
Correct the statement, if it is wrong:
A ray has a definite length.
correct
incorrect
Correct the statement, if it is wrong:
A line segment has a definite length.
Correct
Incorrect
Correct the statement, if it is wrong:
A line has two end-points.
Correct
Incorrect
Correct the statement, if it is wrong:
A ray has only one end point.
Correct
Incorrect
State true or false, if false give the correct statement:
A line has a countable number of points in it.
True
False
State true or false, if false give the correct statement:
Only one line can pass through a given point.
True
False
State true or false, if false give the correct statement:
The intersection of two planes is a straight line
True
False
State, whether the following pair of line or ray appear to be parallel or intersecting.

State, whether the following pair of line or ray appear to be parallel or intersecting.
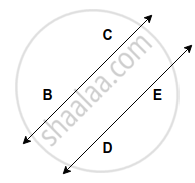
State, whether the following pair of line or ray appear to be parallel or intersecting.

State, whether the following pair of line or ray appear to be parallel or intersecting.
Give two examples, from your surrounding, for the following:
points
Give two examples, from your surrounding, for the following:
line segments
Give two examples, from your surrounding, for the following:
plane surfaces
Give two examples, from your surrounding, for the following:
curved surfaces
Under what condition will two straight lines, in the same plane, have no point in common.
If possible draw a diagram in support of your answer.
Under what condition will two straight lines, in the same plane, have only one point in common.
If possible draw a diagram in support of your answer.
Under what condition will two straight lines, in the same plane, have: an infinite number of points in common.
If possible draw a diagram in support of your answer.
Mark two points A and B on a page of your exercise book. Mark a third point P, such that:
P lies between A and B ; and the three points A, P and B are collinear.
Mark two points A and B on a page of your exercise book. Mark a third point P, such that:
P does not lie between A and B yet the three points are collinear.
Mark two points A and B on a page of your exercise book. Mark a third point P, such that:
the three points do not lie in a line.
Mark two points P and Q on a piece of paper. How many lines can you draw the passing through both the points P and Q?
Mark two points P and Q on a piece of paper. How many lines can you draw the passing through point P?
Mark two points P and Q on a piece of paper. How many lines can you draw the passing through the point Q?
The adjoining diagram shows a line AB. Draw diagram to represent: ray AB i.e. \[\underrightarrow{AB}\]

The adjoining diagram shows a line AB. Draw diagram to represent: \[\underrightarrow{BA}\]
The adjoining diagram shows a line AB. Draw diagram to represent: line segment AB.
The adjoining diagram shows a ray AB. Draw diagrams to show the ray BA i.e. \[\underrightarrow{BA}\]
The adjoining diagram shows a ray AB. Draw diagrams to show the line AB.
The adjoining diagram shows a ray AB. Draw diagrams to show the line segment BA.

The adjoining diagram shows a line segment AB. Draw diagrams to represent the ray AB i.e. \[\underrightarrow{AB}\]
The adjoining diagram shows a ray AB. Draw diagrams to show the line AB i.e. \[\underleftrightarrow{AB}\].
The adjoining diagram shows a line segment AB. Draw diagrams to represent the ray BA.

Use a ruler and whether the following points are collinear or not:
D, A and C
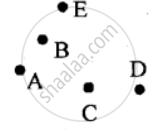
Use a ruler and whether following points are collinear or not:
A, B and C
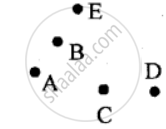
Use a ruler and whether following points are collinear or not:
A, B and E

Use a ruler and whether following points are collinear or not:
B, C and E

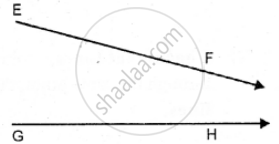
From the adjoining figure, write: all pairs of parallel lines.
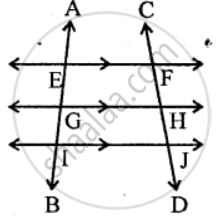
From the adjoining figure, write: all the lines which intersect EF.
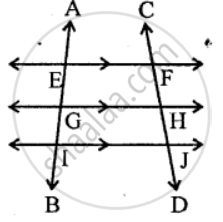
From the adjoining figure, write: lines whose point of intersection is G.
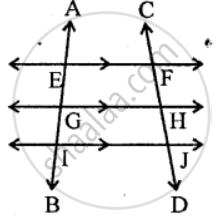
Selina solutions for Mathematics [English] Class 6 23 Fundamental Concepts geometry Exercise 23 (B)
State if the following is a plane closed figure:
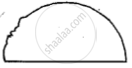
Yes
No
State if the following is a plane closed figure:
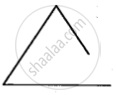
Yes
No
State if the following is a plane closed figure:

Yes
No
State if the following is a plane closed figure:
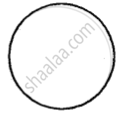
Yes
No
State if the following is a plane closed figure:
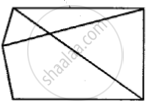
Yes
No
State if the following is a plane closed figure:
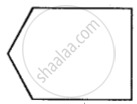
Yes
No
State if the following is a plane closed figure:
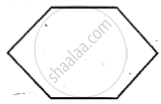
Yes
No
State if the following is a plane closed figure:

Yes
No
Fill in the blank:
______ is a three sided plane closed figure.
Fill in the blank:
A square is a plane closed figure which is not bounded by _______.
Fill in the blank:
A rectangle is a _____ sided plane _______.
Fill in the blank:
A rectangle has opposite sides ______ and adjacent sides ________ to each other.
Fill in the blank:
The sides of a square are ______ to each other and each angle is ____.
Fill in the blank:
For a line segment, a line making the angle of ______ with it, is called perpendicular to it.
Fill in the blank:
For a line segment, a line ______ it and making angle of ______ with it, is called ______ bisector of the line segment.
Fill in the blank:
How many perpendiculars can be drawn to a line segment of length 6 cm?
Fill in the blank:
How many perpendicular bisectors can be drawn to a line segment of length 6 cm?
Fill in the blank:
A perpendicular to a line segment will be its perpendicular bisector if it passes through the _______ of the given line segment.
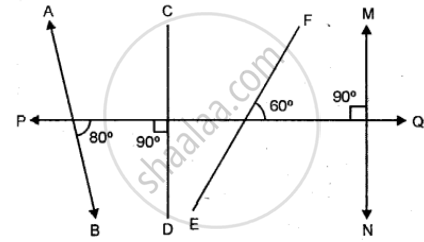
State, which of the lines/line- segments are perpendicular to the line PQ:
State if the following figure shows two mutually perpendicular lines:

Yes
No
State if the following figure shows two mutually perpendicular lines:
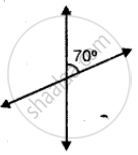
Yes
No
State if the following figure shows two mutually perpendicular lines:

Yes
No
The figure is given below name the line segment that is a perpendicular bisector of the other:
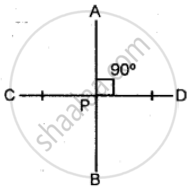
The figure is given below name the line segment that is a perpendicular bisector of the other:
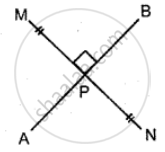
The figure is given below name the line segment that is a perpendicular bisector of the other:
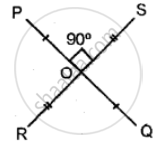
The figure is given below name the line segment that is a perpendicular bisector of the other:
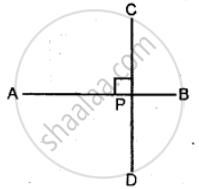
The figure is given below name the line segment that is a perpendicular bisector of the other:
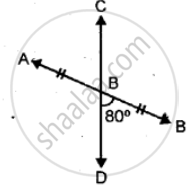
Name three objects from your surroundings that contain perpendicular edges.
Using the given figure, answer the following:
Name the pairs of parallel lines.
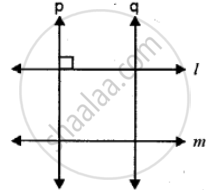
Using the given figure, answer the following:
Name the pairs of mutually perpendicular lines.
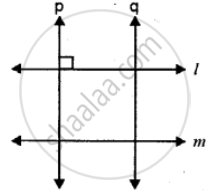
Using the given figure, answer the following:
Is the line p parallel to the line l?
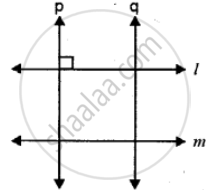
Using the given figure, answer the following:
Is the line q perpendicular to the line m?
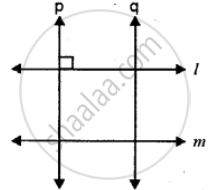
Place a scale (ruler) on a sheet of paper and hold it firmly with one hand. Now draw two line segments AB and CD along the longer edges of the scale. State whether segment AB is parallel to or perpendicular to segment CD.
Check your text book and How many pairs of its edges are parallel to each other ?
Check your text book and How many pairs of its edges are perpendicular to each other?
Give two examples from your surrounding for the following:
intersecting lines
Give two examples from your surrounding for the following:
parallel lines
Give two examples from your surrounding for the following:
perpendicular lines
State true or false; if false, give the correct statement:
The maximum number of lines through three collinear points is three.
True
False
State true or false; if false, give the correct statement:
The maximum number of lines through three non-collinear points is three.
True
False
State true or false; if false, give the correct statement:
Two parallel lines always lie in the same plane.
True
False
State true or false; if false, give the correct statement:
Concurrent lines always meet at the same point.
True
False
State true or false; if false, give the correct statement:
A surface can be plane or curved.
True
False
State true or false; if false, give the correct statement:
There are an infinite number of points in a line segment of length 10 cm.
True
False
State true or false; if false, give the correct statement:
There are an infinite number of points in a line.
True
False
State true or false; if false, give the correct statement:
A plane has an infinite number of lines.
True
False
State true or false; if false, give the correct statement:
A plane has an infinite number of points.
True
False
Selina solutions for Mathematics [English] Class 6 23 Fundamental Concepts geometry Revision Exercise
Mark a point O on a piece of paper. Using a sharp pencil and a ruler, draw a line through the point O. Then draw one more line through the point O. How many lines can you draw through O?
Write a statement regarding your observations.
Mark two points A and B on a plain sheet “ of paper. Using a sharp pencil and a ruler, draw a line through points A and B. Try to draw one more line through A and B. What do you observe?
Write a statement regarding your observations.
Draw two straight lines on a sheet of paper so that the lines drawn the intersect each other.
Draw two straight lines on a sheet of paper so that the lines drawn do not intersect.
Draw two straight lines on a sheet of paper so that the lines drawn appear to intersect when extended.
Draw a figure to show that: points A, B and C arc collinear.
Draw a figure to show that: lines AB, CD and EF are concurrent.
In your note-book, draw two rays with the same initial point O and going in opposite directions. Write the special name for the final figure obtained.
In figure is given below, write the number of line segments used:

In figure is given below, write the number of line segments used:

In figure is given below, write the number of line segments used:

In figure is given below, write the number of line segments used:

In a circle, point P is its centre and PA = PB = radius of the circle. Where do points A and B lie?
Draw a four-sided closed figure, in which all the sides are equal and each angle is 90° and also give the special name of the figure drawn.
Draw a four-sided closed figure, in which opposite sides are equal and each angle is 90° and also give the special name of the figure drawn.
Solutions for 23: Fundamental Concepts geometry
![Selina solutions for Mathematics [English] Class 6 chapter 23 - Fundamental Concepts geometry Selina solutions for Mathematics [English] Class 6 chapter 23 - Fundamental Concepts geometry - Shaalaa.com](/images/mathematics-english-class-6_6:44f3c4f6e33345f4bf41a86d406bf37f.jpg)
Selina solutions for Mathematics [English] Class 6 chapter 23 - Fundamental Concepts geometry
Shaalaa.com has the CISCE Mathematics Mathematics [English] Class 6 CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Mathematics [English] Class 6 CISCE 23 (Fundamental Concepts geometry) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 6 chapter 23 Fundamental Concepts geometry are Concept for Basic Geometrical Ideas (2 -d), Concept for Linkage with and Reflection in Everyday Experiences., Concept for Open and Closed Figures., Concept of Line, Concept for Interior and Exterior of Closed Figures., Curvilinear and Linear Boundaries, Introduction to Basic Concepts in Geometry, Concept of Angle.
Using Selina Mathematics [English] Class 6 solutions Fundamental Concepts geometry exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Mathematics [English] Class 6 students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 23, Fundamental Concepts geometry Mathematics [English] Class 6 additional questions for Mathematics Mathematics [English] Class 6 CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
