Equation of a Plane - Equation of a Plane Passing Through Three Non Collinear Points

Let R, S and T be three non collinear points on the plane with position vectors ${\displaystyle \overrightarrow{a}}$ , ${\displaystyle \overrightarrow{b}}$ and ${\displaystyle \overrightarrow{c}}$ respectively in following fig.

The vectors ${\displaystyle \overrightarrow{RS}}$ and ${\displaystyle \overrightarrow{RT}}$ are in the given plane. Therefore , the vector ${\displaystyle \overrightarrow{RS}\times \overrightarrow{RT}}$ is perpendicular to the plane containing points R,S and T. Let ${\displaystyle \overrightarrow{r}}$be the position vector of any point P in the plane.  Therefore, the equation of the plane passing through R and  perpendicular to the vector  ${\displaystyle \overrightarrow{RS}\times \overrightarrow{RT}}$ is 
${\displaystyle (\overrightarrow{r}-\overrightarrow{a}).(\overrightarrow{RS}\times \overrightarrow{RT})=0}$
or ${\displaystyle (\overrightarrow{r}-\overrightarrow{a}).[(\overrightarrow{b}-\overrightarrow{a})\times (\overrightarrow{c}-\overrightarrow{a})]=0}$  ...(1)
If the three points were on the same line, then there will be many planes that will contain them Fig.

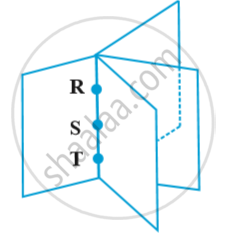
for example , These planes will resemble the pages of a book where the line containing the points R, S and T are members in the binding of the book.

Cartesian form:
Let ${\displaystyle (x_1,y_1,z_1),(x_2,y_2,z_2)}$ and ${\displaystyle (x_3,y_3,z_3)}$  be the coordinates of the points R, S and T respectively.  Let (x, y, z) be the coordinates of any point P on the plane with position vector ${\displaystyle \overrightarrow{r}}$. Then  
${\displaystyle \overrightarrow{RP}=(x-x_1)\hat{i}+(y-y_1)\hat{j}+(z-z_1)\hat{k}}$
${\displaystyle \overrightarrow{RS}=(x_2-x_1)\hat{i}+(y_2-y_1)\hat{j}+(z_2-z_1)\hat{k}}$
${\displaystyle \overrightarrow{RT}=(x_3-x_1)\hat{i}+(y_3-y_1)\hat{j}+(z_3-z_1)\hat{k}}$
Substituting these values in equation (1) of the vector form and expressing it in the form of a determinant, we have 
${\displaystyle \left|\begin{array}{ccc}x-x_1& y-y_1& z-z_1\\ x_2-x_1& y_2-y_1& z_2-z_1\\ x_3-x_1& y_3-y_1& z_3-z_1\end{array}\right|=0}$
which is the equation of the plane in Cartesian form passing through three non collinear points ${\displaystyle (x_1,y_1,z_1),(x_2,y_2,z_2)}$ and ${\displaystyle (x_3,y_3,z_3).}$

Video link : https://youtu.be/PCyo3E5kOcw