Topics
Mathematical Logic
- Statements - Introduction in Logic
- Sentences and Statement in Logic
- Truth Value of Statement
- Open Sentences in Logic
- Compound Statement in Logic
- Quantifier and Quantified Statements in Logic
- Logical Connective, Simple and Compound Statements
- Logical Connective, Simple and Compound Statements
- Examples Related to Real Life and Mathematics
- Statement Patterns and Logical Equivalence
- Algebra of Statements
- Difference Between Converse, Contrapositive, Contradiction
- Application of Logic to Switching Circuits
Mathematical Logic
- Concept of Statements
- Truth Value of Statement
- Logical Connective, Simple and Compound Statements
- Statement Patterns and Logical Equivalence
- Tautology, Contradiction, and Contingency
- Duality
- Quantifier and Quantified Statements in Logic
- Negations of Compound Statements
- Converse, Inverse, and Contrapositive
- Algebra of Statements
- Application of Logic to Switching Circuits
Matrics
- Elementry Transformations
- Inverse of Matrix
- Application of Matrices
- Applications of Determinants and Matrices
Trigonometric Functions
- Trigonometric Equations and Their Solutions
- Solutions of Triangle
- Inverse Trigonometric Functions
Pair of Straight Lines
- Combined Equation of a Pair Lines
- Homogeneous Equation of Degree Two
- Angle between lines represented by ax2 + 2hxy + by2 = 0
- General Second Degree Equation in x and y
- Equation of a Line in Space
Vectors
- Representation of Vector
- Vectors and Their Types
- Algebra of Vectors
- Coplaner Vector
- Vector in Two Dimensions (2-D)
- Three Dimensional (3-D) Coordinate System
- Components of Vector
- Position Vector of a Point P(X, Y, Z) in Space
- Component Form of a Position Vector
- Vector Joining Two Points
- Section Formula
- Scalar Product of Vectors (Dot)
- Vector Product of Vectors (Cross)
- Scalar Triple Product of Vectors
- Vector Triple Product
- Addition of Vectors
Line and Plane
- Vector and Cartesian Equations of a Line
- Distance of a Point from a Line
- Distance Between Skew Lines and Parallel Lines
- Equation of a Plane
- Angle Between Planes
- Coplanarity of Two Lines
- Distance of a Point from a Plane
Linear Programming
- Linear Inequations in Two Variables
- Linear Programming Problem (L.P.P.)
- Lines of Regression of X on Y and Y on X Or Equation of Line of Regression
- Graphical Method of Solving Linear Programming Problems
- Linear Programming Problem in Management Mathematics
Matrices
- Elementary Transformations
- Inverse by Elementary Transformation
- Elementary Transformation of a Matrix Revision of Cofactor and Minor
- Inverse of a Matrix Existance
- Adjoint Method
- Addition of Matrices
- Solving System of Linear Equations in Two Or Three Variables Using Reduction of a Matrix Or Reduction Method
- Solution of System of Linear Equations by – Inversion Method
Differentiation
- Differentiation
- Derivatives of Composite Functions - Chain Rule
- Geometrical Meaning of Derivative
- Derivatives of Inverse Functions
- Logarithmic Differentiation
- Derivatives of Implicit Functions
- Derivatives of Parametric Functions
- Higher Order Derivatives
Applications of Derivatives
- Applications of Derivatives in Geometry
- Derivatives as a Rate Measure
- Approximations
- Rolle's Theorem
- Lagrange's Mean Value Theorem (LMVT)
- Increasing and Decreasing Functions
- Maxima and Minima
Indefinite Integration
Definite Integration
- Definite Integral as Limit of Sum
- Fundamental Theorem of Integral Calculus
- Methods of Evaluation and Properties of Definite Integral
Application of Definite Integration
- Application of Definite Integration
- Area Bounded by the Curve, Axis and Line
- Area Between Two Curves
Differential Equations
- Differential Equations
- Order and Degree of a Differential Equation
- Formation of Differential Equations
- Homogeneous Differential Equations
- Linear Differential Equations
- Application of Differential Equations
- Solution of a Differential Equation
Probability Distributions
- Random Variables and Its Probability Distributions
- Types of Random Variables
- Probability Distribution of Discrete Random Variables
- Probability Distribution of a Continuous Random Variable
- Variance of a Random Variable
- Expected Value and Variance of a Random Variable
Binomial Distribution
- Bernoulli Trial
- Binomial Distribution
- Mean of Binomial Distribution (P.M.F.)
- Variance of Binomial Distribution (P.M.F.)
- Bernoulli Trials and Binomial Distribution
Trigonometric Functions
- Trigonometric equations
- General Solution of Trigonometric Equation of the Type
- Solutions of Triangle
- Hero’s Formula in Trigonometric Functions
- Napier Analogues in Trigonometric Functions
- Inverse Trigonometric Functions
- Inverse Trigonometric Functions - Principal Value Branch
- Graphs of Inverse Trigonometric Functions
- Properties of Inverse Trigonometric Functions
Pair of Straight Lines
- Pair of Lines Passing Through Origin - Combined Equation
- Pair of Lines Passing Through Origin - Homogenous Equation
- Theorem - the Joint Equation of a Pair of Lines Passing Through Origin and Its Converse
- Acute Angle Between the Lines
- Condition for Parallel Lines
- Condition for Perpendicular Lines
- Pair of Lines Not Passing Through Origin-combined Equation of Any Two Lines
- Point of Intersection of Two Lines
Circle
- Tangent of a Circle - Equation of a Tangent at a Point to Standard Circle
- Tangent of a Circle - Equation of a Tangent at a Point to General Circle
- Condition of tangency
- Tangents to a Circle from a Point Outside the Circle
- Director circle
- Length of Tangent Segments to Circle
- Normal to a Circle - Equation of Normal at a Point
Conics
Vectors
- Vectors Revision
- Collinearity and Coplanarity of Vectors
- Linear Combination of Vectors
- Condition of collinearity of two vectors
- Conditions of Coplanarity of Three Vectors
- Section Formula
- Midpoint Formula for Vector
- Centroid Formula for Vector
- Basic Concepts of Vector Algebra
- Scalar Triple Product of Vectors
- Geometrical Interpretation of Scalar Triple Product
- Application of Vectors to Geometry
- Medians of a Triangle Are Concurrent
- Altitudes of a Triangle Are Concurrent
- Angle Bisectors of a Triangle Are Concurrent
- Diagonals of a Parallelogram Bisect Each Other and Converse
- Median of Trapezium is Parallel to the Parallel Sides and Its Length is Half the Sum of Parallel Sides
- Angle Subtended on a Semicircle is Right Angle
Three Dimensional Geometry
Line
Plane
- Equation of Plane in Normal Form
- Equation of Plane Passing Through the Given Point and Perpendicular to Given Vector
- Equation of Plane Passing Through the Given Point and Parallel to Two Given Vectors
- Equation of a Plane Passing Through Three Non Collinear Points
- Equation of Plane Passing Through the Intersection of Two Given Planes
- Vector and Cartesian Equation of a Plane
- Angle Between Two Planes
- Angle Between Line and a Plane
- Coplanarity of Two Lines
- Distance of a Point from a Plane
Linear Programming Problems
Continuity
- Introduction of Continuity
- Continuity of a Function at a Point
- Defination of Continuity of a Function at a Point
- Discontinuity of a Function
- Types of Discontinuity
- Concept of Continuity
- Algebra of Continuous Functions
- Continuity in Interval - Definition
- Exponential and Logarithmic Functions
- Continuity of Some Standard Functions - Polynomial Function
- Continuity of Some Standard Functions - Rational Function
- Continuity of Some Standard Functions - Trigonometric Function
- Continuity - Problems
Differentiation
- Revision of Derivative
- Relationship Between Continuity and Differentiability
- Every Differentiable Function is Continuous but Converse is Not True
- Derivatives of Composite Functions - Chain Rule
- Derivative of Inverse Function
- Derivatives of Inverse Trigonometric Functions
- Derivatives of Implicit Functions
- Exponential and Logarithmic Functions
- Derivatives of Functions in Parametric Forms
- Derivative of Functions in Product of Function Form
- Derivative of Functions in Quotient of Functions Form
- Higher Order Derivative
- Second Order Derivative
Applications of Derivative
- Mean Value Theorem
- Rate of Change of Bodies or Quantities
- Increasing and Decreasing Functions
- Tangents and Normals
- Approximations
- Maxima and Minima - Introduction of Extrema and Extreme Values
- Maxima and Minima in Closed Interval
- Maxima and Minima
Integration
- Methods of Integration: Integration by Substitution
- Methods of Integration: Integration Using Partial Fractions
- Methods of Integration: Integration by Parts
- Definite Integral as the Limit of a Sum
- Fundamental Theorem of Calculus
- Properties of Definite Integrals
- Evaluation of Definite Integrals by Substitution
- Integration by Non-repeated Quadratic Factors
Applications of Definite Integral
Differential Equation
- Differential Equations
- Order and Degree of a Differential Equation
- General and Particular Solutions of a Differential Equation
- Formation of Differential Equation by Eliminating Arbitary Constant
- Differential Equations with Variables Separable Method
- Homogeneous Differential Equations
- Linear Differential Equation
- Applications of Differential Equation
Statistics
Probability Distribution
- Conditional Probability
- Random Variables and Its Probability Distributions
- Discrete and Continuous Random Variable
- Probability Mass Function (P.M.F.)
- Probability Distribution of a Discrete Random Variable
- Cumulative Probability Distribution of a Discrete Random Variable
- Expected Value, Variance and Standard Deviation of a Discrete Random Variable
- Probability Density Function (P.D.F.)
- Distribution Function of a Continuous Random Variable
Bernoulli Trials and Binomial Distribution
- Bernoulli Trials and Binomial Distribution
- Conditions for Binomial Distribution
- Mean of Binomial Distribution (P.M.F.)
- Variance of Binomial Distribution (P.M.F.)
- Standard Deviation of Binomial Distribution (P.M.F.)
- Calculation of Probabilities
- Normal Distribution (P.D.F)
Definition
The angle between a line and a plane is the complement of the angle between the line and normal to the plane Fig.
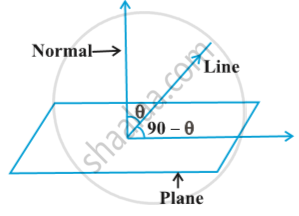
Notes
Vector form If the equation of the line is `vec r = vec a + lambda vec b` and the equation of the plane is `vec r . vec n = d .` Then the angle θ between the line and the normal to the plane is
cos θ = `|(vec b . vec n)/(|vec b| . |vec n|)|`
and so the angle φ between the line and the plane is given by 90 – θ, i.e.,
sin (90 – θ) = cos θ
i.e. sin φ = `|(vec b . vec n)/(|vec b| . |vec n|)|` or
φ =`sin ^ (–1)` `|(bar b . bar n)/(|bar b| . |bar n|)|`
Video link : https://youtu.be/9BKeK0D9unc
If you would like to contribute notes or other learning material, please submit them using the button below.
Shaalaa.com | 3 Dimensional Geometry part 27 (Angle between line and plane)
to track your progress
