Topics
Rational Numbers
- Rational Numbers
- Closure Property of Rational Numbers
- Commutative Property of Rational Numbers
- Associative Property of Rational Numbers
- Distributive Property of Multiplication Over Addition for Rational Numbers
- Identity of Addition and Multiplication of Rational Numbers
- Negative Or Additive Inverse of Rational Numbers
- Concept of Reciprocal or Multiplicative Inverse
- Rational Numbers on a Number Line
- Rational Numbers Between Two Rational Numbers
Linear Equations in One Variable
- Variable of Equation
- Concept of Equation
- Expressions with Variables
- Balancing an Equation
- The Solution of an Equation
- Linear Equation in One Variable
- Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Some Applications Solving Equations Which Have Linear Expressions on One Side and Numbers on the Other Side
- Solving Equations Having the Variable on Both Sides
- Some More Applications on the Basis of Solving Equations Having the Variable on Both Sides
- Reducing Equations to Simpler Form
- Equations Reducible to the Linear Form
Understanding Quadrilaterals
- Concept of Curves
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Classification of Polygons
- Properties of a Quadrilateral
- Interior Angles of a Polygon
- Exterior Angles of a Polygon and Its Property
- Concept of Quadrilaterals
- Properties of Trapezium
- Properties of Kite
- Properties of a Parallelogram
- Properties of Rhombus
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Property: The adjacent angles in a parallelogram are supplementary.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Property: The diagonals of a rhombus are perpendicular bisectors of one another.
- Property: The Diagonals of a Rectangle Are of Equal Length.
- Properties of Rectangle
- Properties of a Square
- Property: The diagonals of a square are perpendicular bisectors of each other.
Practical Geometry
- Introduction to Geometric Tool
- Constructing a Quadrilateral When the Lengths of Four Sides and a Diagonal Are Given
- Constructing a Quadrilateral When Two Diagonals and Three Sides Are Given
- Constructing a Quadrilateral When Two Adjacent Sides and Three Angles Are Known
- Constructing a Quadrilateral When Three Sides and Two Included Angles Are Given
- Some Special Cases
Data Handling
- Concept of Data Handling
- Interpretation of a Pictograph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Organisation of Data
- Frequency Distribution Table
- Graphical Representation of Data as Histograms
- Concept of Pie Graph (Or a Circle-graph)
- Interpretation of Pie Diagram
- Chance and Probability - Chance
- Basic Ideas of Probability
Squares and Square Roots
- Concept of Square Number
- Properties of Square Numbers
- Some More Interesting Patterns of Square Number
- Finding the Square of a Number
- Concept of Square Roots
- Finding Square Root Through Repeated Subtraction
- Finding Square Root Through Prime Factorisation
- Finding Square Root by Division Method
- Square Root of Decimal Numbers
- Estimating Square Root
Cubes and Cube Roots
Comparing Quantities
- Concept of Ratio
- Basic Concept of Percentage
- Increase Or Decrease as Percent
- Concept of Discount
- Estimation in Percentages
- Basic Concepts of Profit and Loss
- Sales Tax, Value Added Tax, and Good and Services Tax
- Calculation of Interest
- Concept of Compound Interest
- Deducing a Formula for Compound Interest
- Rate Compounded Annually Or Half Yearly (Semi Annually)
- Applications of Compound Interest Formula
Algebraic Expressions and Identities
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Like and Unlike Terms
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Multiplication of Algebraic Expressions
- Multiplying Monomial by Monomials
- Multiplying a Monomial by a Binomial
- Multiplying a Monomial by a Trinomial
- Multiplying a Binomial by a Binomial
- Multiplying a Binomial by a Trinomial
- Concept of Identity
- Expansion of (a + b)2 = a2 + 2ab + b2
- Expansion of (a - b)2 = a2 - 2ab + b2
- Expansion of (a + b)(a - b) = a2-b2
- Expansion of (x + a)(x + b)
Mensuration
Visualizing Solid Shapes
Exponents and Powers
Direct and Inverse Proportions
Factorization
- Factors and Multiples
- Factorising Algebraic Expressions
- Factorisation by Taking Out Common Factors
- Factorisation by Regrouping Terms
- Factorisation Using Identities
- Factors of the Form (x + a)(x + b)
- Dividing a Monomial by a Monomial
- Dividing a Polynomial by a Monomial
- Dividing a Polynomial by a Polynomial
- Concept of Find the Error
Introduction to Graphs
- Concept of Bar Graph
- Interpretation of Bar Graphs
- Drawing a Bar Graph
- Concept of Double Bar Graph
- Interpretation of a Double Bar Graph
- Drawing a Double Bar Graph
- Concept of Pie Graph (Or a Circle-graph)
- Graphical Representation of Data as Histograms
- Concept of a Line Graph
- Linear Graphs
- Some Application of Linear Graphs
Playing with Numbers
Definition
- Polyhedron: A polyhedron is a closed space figure whose faces are polygons. A polyhedron is said to be regular if its faces are made up of regular polygons and the same number of faces meet at each vertex.
- Platonic solids: A regular polyhedron is made up of regular polygons. Such solids are also known as ‘platonic solids’.
- Non-polyhedron: A non-polyhedron is not a closed space figure, maybe one or more of the sides is a curved surface.
Notes
Polyhedron:
-
A polyhedron is a closed space figure whose faces are polygons.
-
The word polyhedron has Greek origins, meaning many faces.
-
A solid figure consisting of four or more plane faces (all polygons), pairs of which meet along an edge, three or more edges meeting at a vertex.



-
Each of these solids is made up of polygonal regions which are called its faces; these faces meet at edges which are line segments, and the edges meet at vertices which are points. Such solids are called polyhedrons.
Types of the polyhedron:
-
A polyhedron is said to be regular if its faces are made up of regular polygons and the same number of faces meet at each vertex. any polyhedron that does not meet these conditions is considered irregular.
-
Regular Polyhedron
Irregular Polyhedron
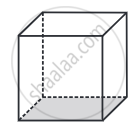
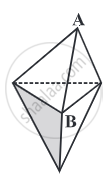
This polyhedron is regular. Its faces are congruent, regular polygons. Vertices are formed by the same number of faces.
This polyhedron is not regular. All the sides are congruent, but the vertices are not formed by the same number of faces. 3 faces meet at A but 4 faces meet at B.
Regular polyhedra:
A regular polyhedron is a polyhedron whose faces are all congruent, regular polygons. A regular polyhedron is named based on its number of faces. There are only five polyhedra that are regular polyhedra; these are referred to as Platonic solids.
The five Platonic solids
Name |
Sketch |
Number of faces |
|
Tetrahedron |
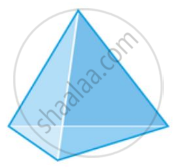 |
4 |
|
Cube |
 |
6 |
|
Octahedron |
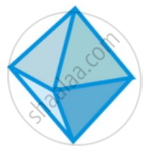 |
8 |
|
Dodecahedron |
 |
12 |
|
Icosahedron |
 |
20 |
In the above table, each regular polyhedra is named based on its number of faces. The net below each sketch shows a 2D picture of all of the faces of the polyhedron.
Non-Polyhedrons:
A non-polyhedron is not a closed space figure, maybe one or more of the sides is a curved surface. Thus, Solids with curved faces are called Non-polyhedrons.
Example: Sphere, Cylinder, Cone, etc.

Concave and Convex polyhedrons:
- Convex Polyhedron: If the surface of a polyhedron does not intersect itself and the line segment connecting any two points of the polyhedron lies within its interior part or surface then such a polyhedron is a convex polyhedron.
- Concave Polyhedron: A non-convex polyhedron is termed as a concave polyhedron.