Advertisements
Advertisements
प्रश्न
A bullet of mass 0.012 kg and horizontal speed 70 m s–1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
उत्तर १
Initial speed of the bullet, ub = 70 m/s
Mass of the wooden block, M = 0.4 kg
Initial speed of the wooden block, uB = 0
Final speed of the system of the bullet and the block = ν
Applying the law of conservation of momentum:
mub + MuB = (m + M) v
0.012 × 70 + 0.4 × 0 = (0.012 + 0.4) v
∴ v = 0.84 / 0.412 = 2.04 m/s
For the system of the bullet and the wooden block:
Mass of the system, m' = 0.412 kg
Velocity of the system = 2.04 m/s
Height up to which the system rises = h
Applying the law of conservation of energy to this system:
Potential energy at the highest point = Kinetic energy at the lowest point
m'gh = (1/2)m'v2
∴ h = (1/2)(v2 / g)
= (1/2) × (2.04)2 / 9.8
= 0.2123 m
The wooden block will rise to a height of 0.2123 m.
Heat produced = Kinetic energy of the bullet – Kinetic energy of the system
= (1/2) mu2 - (1/2) m'v2 = (1/2) × 0.012 × (70)2 - (1/2) × 0.412 × (2.04)2
= 29.4 - 0.857 = 28.54 J
उत्तर २
Here, m1 = 0.012 kg, u1 = 70 m/s
m2 = 0.4 kg, u2 = 0
As the bullet comes to rest with respect to the block, the two behave as one body. Let v be the velocity acquired by the combination.
Applying principle of conservation of linear momentum, (m1 + m2) v = m1H1 + m2u2 = m1u1
`v = (m_1u_1)/(m_1+m_2) = (0.012xx70)/(0.012+0.4) = (0.84)/0.412 = 2.04 ms^(-1)`
Let the block rise to a height h
P.E. of the combination = K.E. of the combination
`(m_1+m_2)gh = 1/2(m_1+m_2)v^2`
`h = v^2/(2g) = (2.04xx2.04)/(2xx9.8) = 0.212 m`
For calculating heat produced, we calculate energy lost (W), where
W = intial K.E. of bullet - final K.E of combination
`= 1/2m_1u_1^2 - 1/2(m_1+m_2)v^2`
`1/2xx0.012(70)^2 - 1/2(0.412)(2.04)`
W = 29.4 - 0.86 = 28.54 joule
:. Heat produced `H = W/J = (28.54)/4.2 = 6.8 cal`
APPEARS IN
संबंधित प्रश्न
The rate of change of total momentum of a many-particle system is proportional to the ______ on the system.
State if the following statement is true or false. Give a reason for your answer.
In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
Define the following:
Coefficient of restitution
A ball of mass 0.1 kg makes an elastic head-on collision with a ball of unknown mass, initially at rest. If the 0 .1 kg ball rebounds at one-third of its original speed, the mass of the other ball is ______.
In inelastic collision, ____________.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
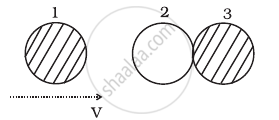
If the collision is elastic, which of the following (Figure) is a possible result after collision?
Two blocks M1 and M2 having equal mass are free to move on a horizontal frictionless surface. M2 is attached to a massless spring as shown in figure. Iniially M2 is at rest and M1 is moving toward M2 with speed v and collides head-on with M2.

- While spring is fully compressed all the KE of M1 is stored as PE of spring.
- While spring is fully compressed the system momentum is not conserved, though final momentum is equal to initial momentum.
- If spring is massless, the final state of the M1 is state of rest.
- If the surface on which blocks are moving has friction, then collision cannot be elastic.
A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that for a general collision, the angle between the two velocities of scattered balls is less than 90°.
Three identical blocks A, B and C are placed on horizontal frictionless surface. The blocks A and C are at rest. But A is approaching towards B with a speed 10 m/s. The coefficient of restitution for all collision is 0.5. The speed of the block C just after the collision is ______.

Answer carefully, with reason:
Is the total linear momentum conserved during the short time of an inelastic collision of two balls ?
