Advertisements
Advertisements
प्रश्न
(a) Can the interference pattern be produced by two independent monochromatic sources of light? Explain.
(b) The intensity at the central maximum (O) in Young's double-slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would `"I"_°/4`
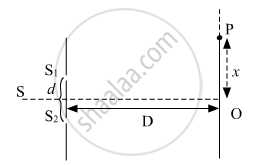
(c) In Young's double-slit experiment, the slits are separated by 0⋅5 mm and the screen is placed 1⋅0 m away from the slit. It is found that the 5th bright fringe is at a distance of 4⋅13 mm from the 2nd dark fringe. Find the wavelength of light used.
उत्तर
(a) Two independent monochromatic sources cannot produce a sustained interference pattern. This is because the phase difference of two independent sources cannot be strictly constant throughout. A constant phase difference is essential to produce a distinguishable interference pattern. [Each of the sources produces their own diffraction pattern which interacts with each other. This interaction may or may not result in the interference pattern in case of 2 different sources but produces a clear pattern in case of coherent sources if d
(b) Fringe width, `beta = lambda"D"/"d"`
Here,
`"OP" ="x" = beta/3 = (lambda"D")/(3"d")`
`"x" = (lambda"D")/(3"d")` ..................(1)
∴ Δ X (Path difference) `= "x""d"/"D"`
∵ `"x""d"/"d" = lambda/3`......(From eq. 1)
⇒ Δ X ` = "x""d"/"D"`
φ (Phase difference) `= (2pi)/(lambda)(Delta "X")`
`= (2pi)/lambda xx lambda / 3 = (2pi)/3`
⇒ φ `= (2pi)/3`
If intensity at point O is IO, then intensity at point P will be,`"I"_"P" = "I"_"O" cos^2 (φ/2)`
`"I"_"P" = "I"_"O" cos^2 (φ/2) = "I"_"O" cos^2(pi/3)`
`= "I"_"O"(1/2)^2 = "I"_"O"/4`
⇒ `"I"_"P" = "I"_"O"/4`
(c) For Young's double slit experiment, Position of 5th bright fringe `=5xx (lambda"D")/"d"`
The position of 2th dark fringe = `(2 xx 2 xx -1) xx (lambda"D")/(2"d") = 1.5 ((lambda"D")/"d")`
Where D is the distance of the screen from the slits and d is the separation between the slits.
According to the given information,
`5 xx ((lambda"D")/"d") - 1.5 xx ((lambda"d")/"d") = 4.13 xx 10^-3 "m"`
⇒ `3.5 xx ((lambda"D")/"d") = 4.13 xx 10^-3 "m"`
⇒ `lambda = (4.13 xx 10^-3 xx 0.5 xx 10^-3)/(3.5xx1) = 0.59 xx 1^-6 "m"`
⇒ `lambda = 590 "nm"`
APPEARS IN
संबंधित प्रश्न
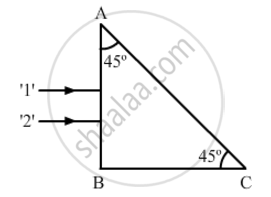
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays '1' and '2' are respectively 1.35 and 1.45. Trace the path of these rays after entering the prism.
What kind of fringes do you expect to observe if white light is used instead of monochromatic light?
When monochromatic light is incident on a surface separating two media, why does the refracted light have the same frequency as that of the incident light?
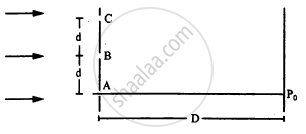
The following figure shows three equidistant slits being illuminated by a monochromatic parallel beam of light. Let \[B P_0 - A P_0 = \lambda/3\text{ and }D > > \lambda.\] (a) Show that in this case \[d = \sqrt{2\lambda D/3}.\] (b) Show that the intensity at P0 is three times the intensity due to any of the three slits individually.
"Monochromatic light should be used to produce pure spectrum". Comment on this statement.
Monochromatic light of wavelength 650 nm falls normally on a slit of width 1.3 x 10-4 cm and the resulting Fraunhofer diffraction is obtained on a screen. Find the angular width of the . central maxima.
Find the angle of incidence at which a ray of monochromatic light should be incident on the first surface AB of a regular glass prism ABC so that the emergent ray grazes the adjacent surface AC. (Refractive Index of glass = 1 .56)
Answer the following question.
In the diffraction due to a single slit experiment, the aperture of the slit is 3 mm. If monochromatic light of wavelength 620 nm is incident normally on the slit, calculate the separation between the first order minima and the 3rd order maxima on one side of the screen. The distance between the slit and the screen is 1.5 m.
Monochromatic light of wavelength 396 nm is incident on the surface of a metal whose work function is 1.125 eV. Calculate:
- the energy of an incident photon in eV.
- the maximum kinetic energy of photoelectrons in eV.
The Figure below shows a ray of monochromatic light LM incident on the first surface AB of a regular (equilateral) glass prism ABC. The emergent ray grazes the adjacent surface AC. Calculate the angle of incidence. (Refractive Index of glass = 1.5)

