Advertisements
Advertisements
प्रश्न
A constant current of 2.8 A exists in a resistor. The rms current is
विकल्प
2.8 A
about 2 A
1.4 A
undefined for a direct current
उत्तर
2.8 A
The constant current is equal to the rms value of current. So,
Irms = 2.8 A
APPEARS IN
संबंधित प्रश्न
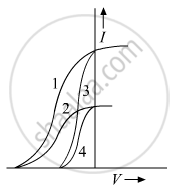
The given graph shows the variation of photo-electric current (I) versus applied voltage (V) for two difference photosensitive materials and for two different intensities of the incident radiations. Identify the pairs of curves that correspond to different materials but same intensity of incident radiation.
In a series LCR circuit connected to an ac source of variable frequency and voltage ν = vm sin ωt, draw a plot showing the variation of current (I) with angular frequency (ω) for two different values of resistance R1 and R2 (R1 > R2). Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced? Define Q-factor of the circuit and give its significance.
Two alternating currents are given by `i_1 = i_0 sin wt and i_2 = i_0 sin (wt + pi/3)` Will the rms values of the currents be equal or different?
Can the peak voltage across the inductor be greater than the peak voltage of the source in an LCR circuit?
Can a hot-wire ammeter be used to measure a direct current of constant value? Do we have to change the graduations?
An alternating current of peak value 14 A is used to heat a metal wire. To produce the same heating effect, a constant current i can be used, where i is
Find the time required for a 50 Hz alternating current to change its value from zero to the rms value.
An electric bulb is designed to operate at 12 volts DC. If this bulb is connected to an AC source and gives normal brightness, what would be the peak voltage of the source?
A capacitor of capacitance 10 μF is connected to an oscillator with output voltage ε = (10 V) sin ωt. Find the peak currents in the circuit for ω = 10 s−1, 100 s−1, 500 s−1 and 1000 s−1.
A coil of inductance 5.0 mH and negligible resistance is connected to the oscillator of the previous problem. Find the peak currents in the circuit for ω = 100 s−1, 500 s−1, 1000 s−1.
A resistor of resistance 100 Ω is connected to an AC source ε = (12 V) sin (250 π s−1)t. Find the energy dissipated as heat during t = 0 to t = 1.0 ms.
The peak voltage of an ac supply is 300 V. What is the rms voltage?
The rms value of current in an ac circuit is 10 A. What is the peak current?
A circuit containing a 80 mH inductor and a 60 µF capacitor in series is connected to a 230 V, 50 Hz supply. The resistance of the circuit is negligible.
(a) Obtain the current amplitude and rms values.
(b) Obtain the rms values of potential drops across each element.
(c) What is the average power transferred to the inductor?
(d) What is the average power transferred to the capacitor?
(e) What is the total average power absorbed by the circuit?
[‘Average’ implies ‘averaged over one cycle’.]
Do the same with the replacement of the earlier transformer by a 40,000-220 V step-down transformer (Neglect, as before, leakage losses though this may not be a good assumption any longer because of the very high voltage transmission involved). Hence, explain why high voltage transmission is preferred?
