Advertisements
Advertisements
प्रश्न
A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of ₹ 4989.60 If the cost of white-washing is ₹ 20 per square meter, find the
- inside surface area of the dome,
- volume of the air inside the dome.
`["Assume "pi=22/7]`
उत्तर
(i) Cost of white-washing the dome from inside = ₹ 4989.60
Cost of white-washing 1 m2 area = ₹ 20
Therefore, the curved surface area of the inner side of the dome = `(4989.60/20) m^2` = 249.48 m2
(ii) Let the inner radius of the hemispherical dome be r.
Curved surface area of the inner side of the dome = 249.48 m2
2πr2 = 249.48 m2
⇒ `2xx22/7 xxr^2=249.48 m^2`
⇒ r2 = `((249.48xx7)/(2xx22))m^2` = 39.69 m2
⇒ r = 6.3 m
The volume of air inside the dome = Volume of the hemispherical dome
= `2/3pir^3`
= `[2/3xx22/7xx(6.3)^3]m^3`
= 523.908 m3
= 523.9 m3 (approximately)
Therefore, the volume of air inside the dome is 523.9 m3.
APPEARS IN
संबंधित प्रश्न
Find the amount of water displaced by a solid spherical ball of diameter 28 cm.
`["Assume "pi=22/7]`
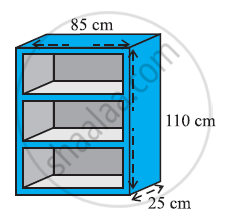
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
A hemispherical bowl is made of steel 0.25 cm thick. The inside radius of the bowl is 5 cm. Find the volume of steel used in making the bowl.
A cylindrical tub of radius 16 cm contains water to a depth of 30 cm. A spherical iron ball is dropped into the tub and thus level of water is raised by 9 cm. What is the radius of the ball?
A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1 .5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimetres?
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
A sphere, a cylinder and a cone have the same diameter. The height of the cylinder and also the cone are equal to the diameter of the sphere. Find the ratio of their volumes.
Find the radius of a sphere if its volume is 904.32 cubic cm. (π = 3.14)
The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
