Advertisements
Advertisements
प्रश्न
A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground based observer?
उत्तर
Vrg is the velocity of rain that appears to the girl.
We must draw all vectors in the reference frame of the ground-based observer.
Assume north to be `hati` direction and vertically downward to be `(-hatj)`.
Let the rain velocity `v_r = ahati + bhatj`'
Case I: According to the problem, velocity of girl `v_g = ((5m)/s)hati`
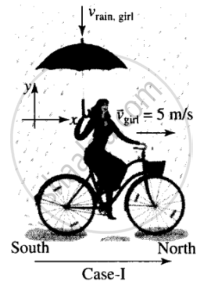
Let `v_(rg)` = velocity of rain w.r.t. girl
= `v_r - v_g`
= `(ahati + bhatj) - 5hati`
= `(a - 5)hati + bhatj`
According to the question, rain appears to fall vertically downward.
Hence, `a - 5 = 0 ⇒ 4a = 5`
Case II: Now velocity of the girl after increasing her speed,
`v_g = ((10m)/s)hati`
∴ `v_(rg) = v_r - v_g`
= `(ahati + bhatj) - 10hati`
= `(a - 10)hati + bhatj`
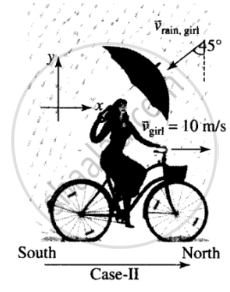
According to the question, rain appears to fall at 45 to the vertical.
Hence `tan 45^circ = b/(a - 10)` = 1
⇒ `b = a - 10`
= `5 - 10`
= `- 5`
Hence, velocity of rain = `ahati + bhatj`
⇒ `v_r = 5hati - 5hatj`
Speed of rain
= `|v_r| = sqrt((5)^2 + (-5)^2`
= `sqrt(50)`
= `5sqrt(2)` m/s.
APPEARS IN
संबंधित प्रश्न
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
A body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If the second body of mass of 4 m is projected horizontally from the top of a tower of the height of 4 h, it reaches the ground at a distance of 4x from the foot of the tower. The horizontal velocity of the second body is:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be ______.
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
- greatest speed.
- smallest speed.
- greatest acceleration?
Explain
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
Average torque on a projectile of mass m, initial speed u and angle of projection θ between initial and final positions P and Q as shown in figure about the point of projection is ______.