Advertisements
Advertisements
प्रश्न
A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground based observer?
उत्तर
Vrg is the velocity of rain that appears to the girl.
We must draw all vectors in the reference frame of the ground-based observer.
Assume north to be `hati` direction and vertically downward to be `(-hatj)`.
Let the rain velocity `v_r = ahati + bhatj`'
Case I: According to the problem, velocity of girl `v_g = ((5m)/s)hati`
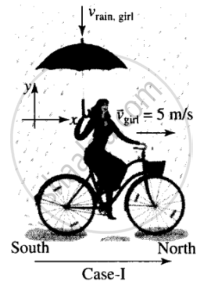
Let `v_(rg)` = velocity of rain w.r.t. girl
= `v_r - v_g`
= `(ahati + bhatj) - 5hati`
= `(a - 5)hati + bhatj`
According to the question, rain appears to fall vertically downward.
Hence, `a - 5 = 0 ⇒ 4a = 5`
Case II: Now velocity of the girl after increasing her speed,
`v_g = ((10m)/s)hati`
∴ `v_(rg) = v_r - v_g`
= `(ahati + bhatj) - 10hati`
= `(a - 10)hati + bhatj`
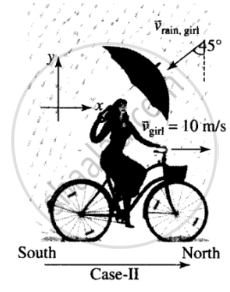
According to the question, rain appears to fall at 45 to the vertical.
Hence `tan 45^circ = b/(a - 10)` = 1
⇒ `b = a - 10`
= `5 - 10`
= `- 5`
Hence, velocity of rain = `ahati + bhatj`
⇒ `v_r = 5hati - 5hatj`
Speed of rain
= `|v_r| = sqrt((5)^2 + (-5)^2`
= `sqrt(50)`
= `5sqrt(2)` m/s.
APPEARS IN
संबंधित प्रश्न
A man can swim with a speed of 4.0 km/h in still water. How long does he take to cross a river 1.0 km wide if the river flows steadily at 3.0 km/h and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?
A ball rolls of the top of the stairway with a horizontal velocity u ms−1. If the steps are h m high and b m wide, the ball will hit the edge of the nth step, if:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
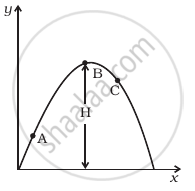
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of (18 km/h). Give explanation to support your diagram.
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
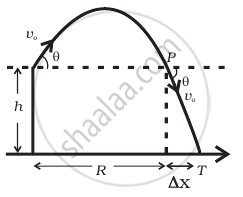
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
