Advertisements
Advertisements
प्रश्न
A golf ball has diameter equal to 4.2 cm. Its surface has 200 dimples each of radius 2 mm. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.
उत्तर
Surface area of ball
`=4pir^2`
`=4pi (4.2 /2)^2`
`= 17.64 pi cm^2`
Total surface area exposed
SA of ball `- 200 (pir^2 - (4pir^2)/2)`
`=17.64 pi - 200 pir^2`
`=17.64 pi -8pi`
`= 80.5 cm^2`
APPEARS IN
संबंधित प्रश्न
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use \[\pi = \frac{22}{7}\]]
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
The radius of the base of a right circular cone of semi-vertical angle α is r. Show that its volume is \[\frac{1}{3} \pi r^3\] cot α and curved surface area is πr2 cosec α.
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The sum of length, breadth and height of a cuboid is 19 cm and its diagonal is `5sqrt(5)` cm. Its surface area is
The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. Find the curved surface area of the bucket.
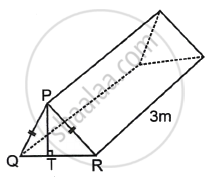
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent