Advertisements
Advertisements
प्रश्न
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
उत्तर
Volume of cylinder = `pir^2 h`
`=22/7 xx 7/2 xx 7/2 xx 12`
`=462 xm^3`
Volume of 2 hemisphere = `4pir^3`
`=4/3 xx 22/7 xx 7/2 xx 7/2 xx 7/2`
`=179.6 cm^3`
Therefore,
Volume of solid `=462 + 179.6`
`=641.6 cm^3`
Total surface area of the solid
`=2pirh + 4pir^2`
`= 2pir (h +2r)`
`= 2 xx 22/7 xx 7/2 (12 + 2 xx 7/2)`
`= 418 cm^2`
APPEARS IN
संबंधित प्रश्न
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is 10459 `3/7` cm3. The radii of its lower and upper circular ends are 8cm and 20cm. find the cost of metal sheet used in making container at rate of Rs 1.4 per cm2?
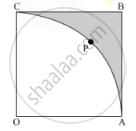
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
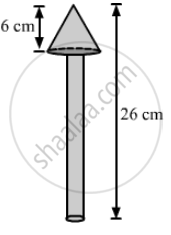
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
Five identical cubes, each of edge 5 cm, are placed adjacent to each other. Find the volume of the resulting cuboid.
Match the following columns:
| Column I | Column II |
| (a) The radii of the circular ends of a bucket, in the form of the frustum of a cone of height 30 cm, are 20 cm and 10 cm respectively. The capacity of the bucket is ........cm3. |
(p) 2418π |
| (b) The radii of the circular ends of a conical bucket of height 15 cm are 20 and 12 cm respectively. The slant height of the bucket is ........ cm. |
(q) 22000 |
| (c) The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. The total surface area of the bucket is .........cm2. |
(r) 12 |
| (d) Three solid metallic spheres of radii 3 cm, 4 cm and 5 cm are melted to form a single solid sphere. The diameter of the resulting sphere is ........ cm. |
(s) 17 |
Two cubes each of volume 8 cm³ are joined end to end, then the surface area of the resulting cuboid is ______.
The total surface area of a solid hemisphere of radius r is ________.
If two solid hemispheres of the same base radius r are joined together along their bases, then curved surface area of this new solid is ______.
|
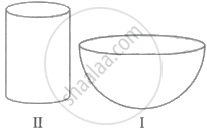
Khurja is a city in the Indian state of Uttar Pradesh famous for the pottery. Khurja pottery is traditional Indian pottery work which has attracted Indians as well as foreigners with a variety of tea sets, crockery and ceramic tile works. A huge portion of the ceramics used in the country is supplied by Khurja and is also referred as "The Ceramic Town". One of the private schools of Bulandshahr organised an Educational Tour for class 10 students to Khurja. Students were very excited about the trip. Following are the few pottery objects of Khurja.
Students found the shapes of the objects very interesting and they could easily relate them with mathematical shapes viz sphere, hemisphere, cylinder etc. |
Maths teacher who was accompanying the students asked the following questions:
- The internal radius of hemispherical bowl (filled completely with water) in I is 9 cm and the radius and height of the cylindrical jar in II are 1.5 cm and 4 cm respectively. If the hemispherical bowl is to be emptied in cylindrical jars, then how many cylindrical jars are required?
- If in the cylindrical jar full of water, a conical funnel of the same height and same diameter is immersed, then how much water will flow out of the jar?
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is `7/2` m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.