Advertisements
Advertisements
प्रश्न
Find the mass of a 3.5 m long lead pipe, if the external diameter of the pipe is 2.4 cm, thickness of the metal is 2 mm and the mass of 1 cm3 of lead is 11.4 grams.
उत्तर
Length of the pipe (h) = 3.5 cm = 300 cm
External radius of the pipe (R) = \[\frac{2 . 4}{2} = 1 . 2 cm\]
Thickness of pipe = 2 mm
= 0.2 cm
So internal radius of pipe = 1.2 - 0.2
= 1cm
Thus volume of pipe `=pi(R^2 - r^2)h`
`=22/7 xx ((1.2)^2 - 1^2) xx 300`
`=22 xx 50 xx 0.44 cm^3`
`=484 cm^3`
Mass of 1 cm3 pipe is 11.4 gm
Total mass = 4184 × 11.4 = 5517.6 gm = 5.518 kg.
APPEARS IN
संबंधित प्रश्न
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3 `5/9` cm. Find the diameter of the cylindrical vessel.
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
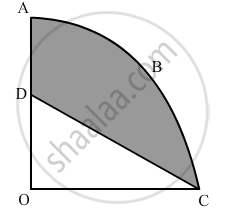
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the volume of wood in the toy. `[\text{Use}pi 22/7]`
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m × 16 m × 11 m.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
The surface area of a sphere is same as the curved surface area of a right circular cylinder whose height and diameter are 12 cm each. The radius of the sphere is
The radii of the circular ends of a bucket of height 15 cm are 14 cm and r cm (r < 14). If the volume of bucket is 5390 cm3, then find the value of r.
The surface area of a sphere is 154 cm2. The volume of the sphere is
