Advertisements
Advertisements
प्रश्न
The surface area of a sphere is 154 cm2. The volume of the sphere is
विकल्प
`"179"2/3 "cm"^3`
`"359"1/3"cm"^3`
`"1437"1/3"cm"^3`
None of these
उत्तर
`"179"2/3"cm"^3`
surface area of a sphere = 4πr2
Therefore,
4πr2 = 154
`=> 4xx22/7xx"r"^2 = 154`
`=> "r"^2 = (154xx7/88)`
`=> "r"^2 = 49/4`
`=> "r"^2 = (7/2)^2`
`=> r = 7/2 "cm"`
Volume of the sphere `=4/3pi"r"^3`
`= "Volume of the sphere" = 4/3 pi"r"^3`
`= 539/3 "cm"^3`
`= 179 2/3 "cm"^2`
APPEARS IN
संबंधित प्रश्न
To fill a swimming pool two pipes are to be used. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool.
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
In the middle of a rectangular field measuring 30 m × 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
A hemispherical bowl of internal radius 15 cm contains a liquid. The liquid is to be filled into cylindrical-shaped bottles of diameter 5 cm and height 6 cm. How many bottles are necessary to empty the bowl?
Water flows at the rate of 10 metre per minute from a cylindrical pipe 5 mm in diameter. How long will it take to fill up a conical vessel whose diameter at the base is 40 cm and depth 24 cm?
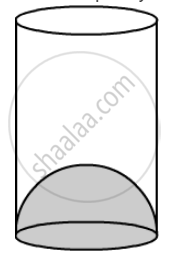
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
A hemispherical bowl of internal radius 9 cm is full of water. Its contents are emptied into a cylindrical vessel of internal radius 6 cm. Find the height of water in the cylindrical vessel.
A river 1.5 m deep and 36 m wide is flowing at the rate of 3.5 km/hr. Find the amount of water (in cubic metres) that runs into the sea per minute.
The height of a conical tent is 14 m and its floor area is 346.5 m2. How much canvas, 1.1 wide, will be required for it?
The curved surface area of a right circular cone is 12320 cm2. If the radius of its base is 56 cm, then find its height.
