Advertisements
Advertisements
प्रश्न
A graph representing the function f(x) is given in it is clear that f(9) = 2
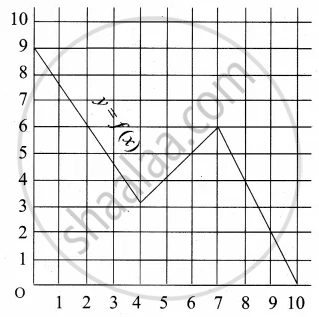
Describe the following Range
उत्तर
Range = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
= {x / 0 ≤ x ≤ 9, x ∈ R}
APPEARS IN
संबंधित प्रश्न
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(b) {x : f(x) = −2}
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
Check if the following relation is function:
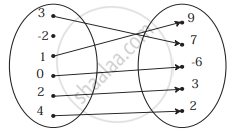
Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
Write the following expression as sum or difference of logarithm
`log (sqrt(x) root(3)(y))`
A graph representing the function f(x) is given in it is clear that f(9) = 2
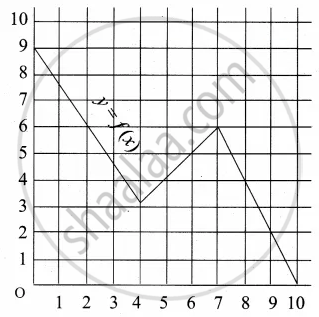
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
If f(x) = 5x - 3, then f-1(x) is ______
Find the range of the following functions given by `|x - 4|/(x - 4)`
Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to ______.
