Advertisements
Advertisements
प्रश्न
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
विकल्प
(a) cos (x − y)
(b) log (cos (x − y))
(c) 1
(d) cos (x + y)
(e) 0
उत्तर
Given:
\[ \Rightarrow f\left( \frac{1}{x} \right) = \cos\left( - \log_e \left( x \right) \right)\]
\[ \Rightarrow f\left( \frac{1}{x} \right) = \cos\left( \log_e \left( x \right) \right)\]
\[ \Rightarrow f\left( \frac{x}{y} \right) + f\left( xy \right) = 2\cos\left( \log_e x \right)\cos\left( \log_e y \right)\]
\[ \Rightarrow \frac{1}{2}\left[ f\left( \frac{x}{y} \right) + f\left( xy \right) \right] = \cos\left( \log_e x \right)\cos\left( \log_e y \right)\]
Notes
Disclaimer: The question in the book has some error, so none of the options are matching with the solution. The solution is created according to the question given in the book.
APPEARS IN
संबंधित प्रश्न
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
- {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
- {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
- {(1, 3), (1, 5), (2, 5)}
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
If f, g and h are real functions defined by
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
Write the domain and range of function f(x) given by
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
Let f and g be two functions given by
f = {(2, 4), (5, 6), (8, −1), (10, −3)} and g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, −5)}.
Find the domain of f + g
If f(x) = cos (log x), then the value of f(x2) f(y2) −
The range of f(x) = cos [x], for π/2 < x < π/2 is
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
If f(m) = m2 − 3m + 1, find f(x + 1)
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
e–x = 6
Find the domain of f(x) = log10 (x2 − 5x + 6)
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
The equation logx2 16 + log2x 64 = 3 has,
Answer the following:
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 5
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
Let f : R → R be given by f(x) = x3 + 1 for all x ∈ R. Draw its graph
Answer the following:
Find x, if x = 33log32
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the domain of the following function.
f(x) = 5–xPx–1
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
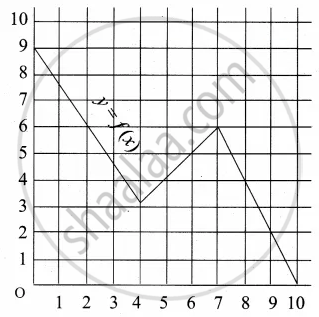
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
Domain of `sqrt(a^2 - x^2) (a > 0)` is ______.
The domain and range of the real function f defined by f(x) = `(4 - x)/(x - 4)` is given by ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
