Advertisements
Advertisements
Question
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
Options
(a) cos (x − y)
(b) log (cos (x − y))
(c) 1
(d) cos (x + y)
(e) 0
Solution
Given:
\[ \Rightarrow f\left( \frac{1}{x} \right) = \cos\left( - \log_e \left( x \right) \right)\]
\[ \Rightarrow f\left( \frac{1}{x} \right) = \cos\left( \log_e \left( x \right) \right)\]
\[ \Rightarrow f\left( \frac{x}{y} \right) + f\left( xy \right) = 2\cos\left( \log_e x \right)\cos\left( \log_e y \right)\]
\[ \Rightarrow \frac{1}{2}\left[ f\left( \frac{x}{y} \right) + f\left( xy \right) \right] = \cos\left( \log_e x \right)\cos\left( \log_e y \right)\]
Notes
Disclaimer: The question in the book has some error, so none of the options are matching with the solution. The solution is created according to the question given in the book.
APPEARS IN
RELATED QUESTIONS
Define a function as a correspondence between two sets.
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(a) the image set of the domain of f
If f(x) = x2, find \[\frac{f\left( 1 . 1 \right) - f\left( 1 \right)}{\left( 1 . 1 \right) - 1}\]
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If \[f\left( x \right) = \frac{x + 1}{x - 1}\] , show that f[f[(x)]] = x.
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If f, g and h are real functions defined by
Write the domain and range of \[f\left( x \right) = \sqrt{x - \left[ x \right]}\] .
Find the set of values of x for which the functions f(x) = 3x2 − 1 and g(x) = 3 + x are equal.
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right)\] , then \[f\left( \frac{2x}{1 + x^2} \right)\] is equal to
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
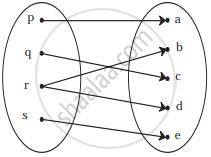
Check if the following relation is function:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
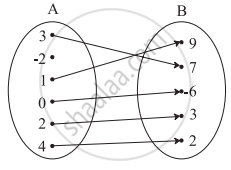
Check if the following relation is a function.
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x3
Express the following logarithmic equation in exponential form
log10 (0.001) = −3
If `log((x + y)/3) = 1/2 log x + 1/2 logy`, show that `x/y + y/x` = 7
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range
{(12, 1), (3, 1), (5, 2)}
Answer the following:
Let f : R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph
Answer the following:
If f(x) = log(1 – x), 0 ≤ x < 1 show that `"f"(1/(1 + x))` = f(1 – x) – f(– x)
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
If a2 = b3 = c4 = d5, show that loga bcd = `47/30`
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A function f is defined by f(x) = 2x – 3 find x such that f(x) = 0
Range of f(x) = `1/(1 - 2 cosx)` is ______.
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
